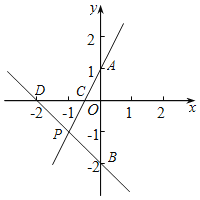题目内容
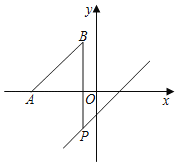
【题目】如图,在平面直角坐标系xOy中,点B(﹣1,3),点A(﹣5,0),点P是直线y=x﹣2上一点,且∠ABP=45°,则点P的坐标为_____.
【答案】(﹣2,﹣4)
【解析】
将线段BA绕点B逆时针旋转90°得到线段BA′,则A′(2,﹣1),取AA′的中点K(﹣![]() ,﹣
,﹣![]() ),直线BK与直线y=x﹣2的交点即为点P.求出直线BK的解析式,利用方程组确定交点P坐标即可
),直线BK与直线y=x﹣2的交点即为点P.求出直线BK的解析式,利用方程组确定交点P坐标即可
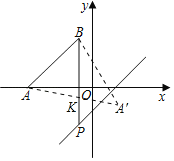
解:将线段BA绕点B逆时针旋转90°得到线段BA′,则A′(2,﹣1),
取AA′的中点K(﹣![]() ,﹣
,﹣![]() ),
),
直线BK与直线y=x﹣2的交点即为点P.
设直线PB的解析式为y=kx+b,
把B(﹣1,3),K(﹣![]() ,﹣
,﹣![]() )代入得
)代入得 ,
,
解得![]()
∵直线BK的解析式为y=7x+10,
由![]() ,
,
解得![]() ,
,
∴点P坐标为(﹣2,﹣4),
故答案为(﹣2,﹣4).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目