题目内容
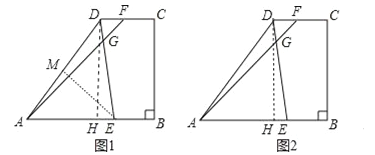
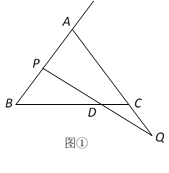
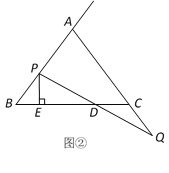
【题目】如图所示，梯形ABCD中，AB∥DC，∠B=90°，AD=15，AB=16，BC=12，点E是边AB上的动点，点F是射线CD上一点，射线ED和射线AF交于点G，且∠AGE=∠DAB．
（1）求线段CD的长；
（2）如果△AEG是以EG为腰的等腰三角形，求线段AE的长；
（3）如果点F在边CD上（不与点C、D重合），设AE=x，DF=y，求y关于x的函数解析式，并写出x的取值范围．
【答案】答案见解析.
【解析】
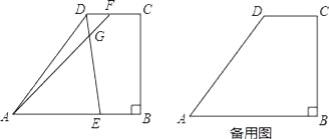
试题（1）作DH⊥AB于H，如图1，易得四边形BCDH为矩形，则DH=BC=12，CD=BH，再利用勾股定理计算出AH，从而得到BH和CD的长；
（2）分类讨论：当EA=EG时，则∠AGE=∠GAE，则判断G点与D点重合，即ED=EA，作EM⊥AD于M，如图1，则AM=
AD=
，通过证明Rt△AME∽Rt△AHD，利用相似比可计算出此时的AE长；当GA=GE时，则∠AGE=∠AEG，可证明AE=AD=15，（3）作DH⊥AB于H，如图2，则AH=9，HE=AE﹣AH=x﹣9，先利用勾股定理表示出DE=
，再证明△EAG∽△EDA，则利用相似比可表示出EG=
，则可表示出DG，然后证明△DGF∽△EGA，于是利用相似比可表示出x和y的关系．
试题解析：（1）作DH⊥AB于H，如图1，易得四边形BCDH为矩形，∴DH=BC=12，CD=BH，在Rt△ADH中，AH=
=
=9，∴BH=AB﹣AH=16﹣9=7，∴CD=7；
（2）当EA=EG时，则∠AGE=∠GAE，∵∠AGE=∠DAB，∴∠GAE=∠DAB，∴G点与D点重合，即ED=EA，作EM⊥AD于M，如图1，则AM=AD=，∵∠MAE=∠HAD，∴Rt△AME∽Rt△AHD，∴AE：AD=AM：AH，即AE：15=：9，解得AE=
；
当GA=GE时，则∠AGE=∠AEG，∵∠AGE=∠DAB，而∠AGE=∠ADG+∠DAG，∠DAB=∠GAE+∠DAG，∴∠GAE=∠ADG，∴∠AEG=∠ADG，∴AE=AD=15，综上所述，△AEC是以EG为腰的等腰三角形时，线段AE的长为或15；
（3）作DH⊥AB于H，如图2，则AH=9，HE=AE﹣AH=x﹣9，在Rt△ADE中，DE=
=，∵∠AGE=∠DAB，∠AEG=∠DEA，∴△EAG∽△EDA，∴EG：AE=AE：ED，即EG：x=x：，∴EG=，∴DG=DE﹣EG=
，∵DF∥AE，∴△DGF∽△EGA，∴DF：AE=DG：EG，即y：x=（）：，∴
（9＜x＜）．
