题目内容
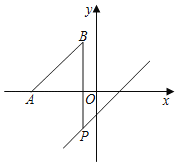
【题目】如图,已知直线l1:y1=2x+1与坐标轴交于A、C两点,直线l2:y2=﹣x﹣2与坐标轴交于B、D两点,两直线的交点为P点.
(1)求P点的坐标;
(2)求△APB的面积;
(3)x轴上存在点T,使得S△ATP=S△APB,求出此时点T的坐标.
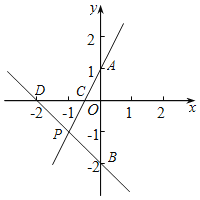
【答案】(1)P(﹣1,﹣1);(2)![]() ;(3)T(1,0)或(﹣2,0).
;(3)T(1,0)或(﹣2,0).
【解析】
(1)解析式联立构成方程组,该方程组的解就是交点坐标;
(2)利用三角形的面积公式解答;
(3)求得C的坐标,因为S△ATP=S△APB,S△ATP=S△ATC+S△PTC=|x+![]() |,所以|x+
|,所以|x+![]() |=
|=![]() ,解得即可.
,解得即可.
解:(1)由![]() ,解得
,解得![]() ,
,
所以P(﹣1,﹣1);
(2)令x=0,得y1=1,y2=﹣2
∴A(0,1),B(0,﹣2),
则 S△APB=![]() ×(1+2)×1=
×(1+2)×1=![]() ;
;
(3)在直线l1:y1=2x+1中,令y=0,解得x=﹣![]() ,
,
∴C(﹣![]() ,0),
,0),
设T(x,0),
∴CT=|x+![]() |,
|,
∵S△ATP=S△APB,S△ATP=S△ATC+S△PTC=![]() |x+
|x+![]() |(1+1)=|x+
|(1+1)=|x+![]() |,
|,
∴|x+![]() |=
|=![]() ,
,
解得x=1或﹣2,
∴T(1,0)或(﹣2,0).

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目