题目内容
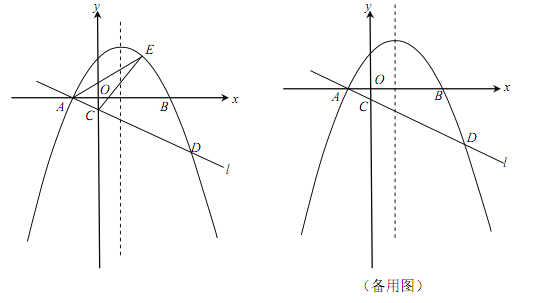
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点.
与x轴交于A、B两点,与y轴交于C点.
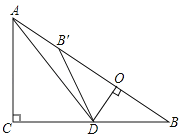
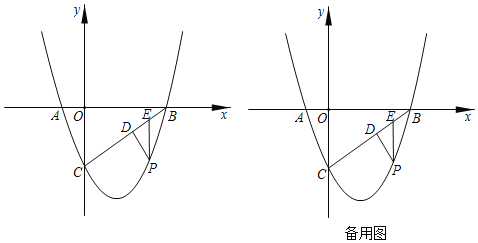
(1)点P是线段BC下方的抛物线上一点,过点P作PD⊥BC交BC于点D,过点P作EP∥y轴交BC于点E.点MN是直线BC上两个动点且MN=AO(xM<xN).当DE长度最大时,求PM+MN﹣![]() BN的最小值.
BN的最小值.
(2)将点A向左移动3个单位得点G,△GOC延直线BC平移运动得到三角形△G'O′C'(两三角形可重合),则在平面内是否存在点G',使得△G′BC为等腰三角形,若存在,直接写出满足条件的所有点G′的坐标,若不存在请说明理由.
【答案】(1)![]() ;(2)点G′(﹣4,0)或(﹣
;(2)点G′(﹣4,0)或(﹣![]() ,
,![]() ).
).
【解析】
(1)DE=PEsin∠EPD=![]() (
(![]() x﹣
x﹣![]() ﹣
﹣![]() x2+
x2+![]() x+
x+![]() ),当x=2时,DE最大,此时点P(2,﹣
),当x=2时,DE最大,此时点P(2,﹣![]() );MN=AO=1,将△BCO沿BC翻折得到△BCO′,将点P沿CB的方向平移1个单位得到点P′(
);MN=AO=1,将△BCO沿BC翻折得到△BCO′,将点P沿CB的方向平移1个单位得到点P′(![]() ,
,![]() ),作P′H⊥BO′交BO′于点H,交BC于点N,将点N沿BC方向平移1个单位得到点M,则点M、N为所求,即可求解;
),作P′H⊥BO′交BO′于点H,交BC于点N,将点N沿BC方向平移1个单位得到点M,则点M、N为所求,即可求解;
(2)分BC=BG′、BC=G′C、BG=CG′三种情况,分别求解即可.
(1)y=![]() =
=![]() (x﹣4)(x+1),
(x﹣4)(x+1),
故点A、B、C的坐标分别为:(﹣1,0)、(4,0)、(0,﹣![]() );
);
则直线BC的表达式为:y=![]() (x﹣4);
(x﹣4);
设点P(x,![]() ),则点E(x,
),则点E(x,![]() x﹣
x﹣![]() ),
),
∵![]() ,∠EPD=∠OBC,
,∠EPD=∠OBC,
∴DE=PEsin∠EPD=![]() (
(![]() x﹣
x﹣![]() ﹣
﹣![]() x2+
x2+![]() x+
x+![]() ),
),
当x=2时,DE最大,此时点P(2,﹣![]() );
);
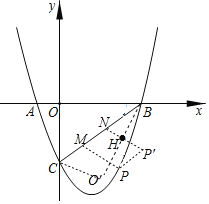
MN=AO=1,将△BCO沿BC翻折得到△BCO′,
将点P沿CB的方向平移1个单位得到点P′(![]() ,
,![]() ),作P′H⊥BO′交BO′于点H,交BC于点N,
),作P′H⊥BO′交BO′于点H,交BC于点N,
将点N沿BC方向平移1个单位得到点M,则点M、N为所求;
P′P∥MN,且PP′=MN,则四边形P′PNM为平行四边形,则P′N=PM,
∠CBO′=∠OBC=30°,则HN=NBsin30![]() =
=![]() BN,
BN,
PM+MN﹣![]() BN=MN+P′N﹣
BN=MN+P′N﹣![]() BN=MN+P′H为最小;
BN=MN+P′H为最小;
直线BO′的倾斜角为60°,则其表达式为:y=![]() (x﹣4)…①,
(x﹣4)…①,
则直线P′N表达式中的k为:﹣![]() ,其表达式为:y=﹣
,其表达式为:y=﹣![]() x+b,
x+b,
将点P′坐标代入并解得:
直线P′N的表达式为:y=﹣![]() x+
x+![]() …②,
…②,
联立①②并解得:x=![]() ,故点H(
,故点H(![]() ,
,![]() );
);
P′H=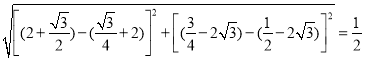 ,
,
PM+MN﹣![]() BN最小值=MN+P′N﹣
BN最小值=MN+P′N﹣![]() BN=MN+P′H=
BN=MN+P′H=![]() ;
;
(2)直线BC的表达式为:y=![]() (x﹣4);点G(﹣4,0),
(x﹣4);点G(﹣4,0),
设△GOC沿直线BC向上平移m个单位,则向右平移![]() m个单位,则点G′(m﹣4,
m个单位,则点G′(m﹣4,![]() m);
m);
BC2=![]() ,BG′2=(m﹣8)2+3m2,CG′2=(m﹣4)2+(
,BG′2=(m﹣8)2+3m2,CG′2=(m﹣4)2+(![]() m+
m+![]() )2=4m2+
)2=4m2+![]() ;
;
①当BC=BG′时,BC2=(m﹣8)2+3m2,方程无解;
②当BC=G′C时,同理可得:m=0;
③当BG=CG′时,同理可得:m=![]() ;
;
即m=0或![]() ,
,
故点G′(﹣4,0)或(﹣![]() ,
,![]() ).
).

 备战中考寒假系列答案
备战中考寒假系列答案