题目内容
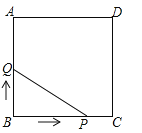
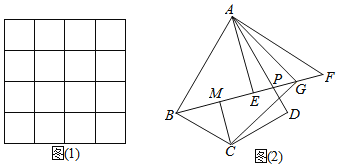
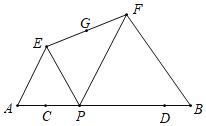
【题目】已知线段AB＝12，C、D是AB上两点，且AC＝DB＝2，P是线段CD上一动点，在AB同侧分别作等边三角形APE和等边三角形PBF，G为线段EF的中点，点P由点C移动到点D时，G点移动的路径长度为_____
【答案】4
【解析】
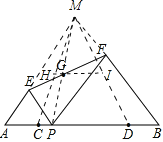
分别延长AE、BF交于点M，易证四边形PEMF为平行四边形，得出G为PM中点，则G的运行轨迹为△MCD的中位线，运用中位线的性质求出HI的长度即可．
解：如图，分别延长AE、BF交于点M，
∵∠A＝∠DPF＝60°，
∴AM∥PF，
∵∠B＝∠EPA＝60°，
∴BM∥PE，
∴四边形PEMF为平行四边形，
∴EF与MP互相平分．
∵G为EF的中点，
∴G正好为PM的中点，
即在P的运动过程中，G始终为PM的中点，
∴G的运行轨迹为△MCD的中位线HI，
∵HI＝
CD＝×（12﹣2﹣2）＝4，
∴G点移动的路径长度为4．
故答案为：4
练习册系列答案
相关题目
