Question

【题目】在锐角中，边长长为18，高长为12．

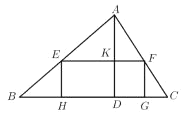
（1）如图，矩形的边在边上，其余两个顶点、分别在、边上，交于点，求的值．

（2）设，矩形的面积为，求于的函数关系式，并求的最大值．

Answer 1

【答案】（1）；（2），当时，有最大值为54．

【解析】

（1）由矩形的性质得出EF//BC，从而得，根据相似三角形对应高的比等于相似比可得，继而根据比例的性质即可求得答案；

（2）由已知可得四边形EHDK是矩形，从而得KD=EH=x，继而得出，，再根据矩形的面积公式可得函数关系式，继而利用二次函数的性质即可求得面积的最大值．

（1）∵四边形EFGH是矩形，边GH在BC边上，

∴EF//BC，

又∵AD⊥BC，

∴AK⊥EF，

∵EF//BC，

∴，

∴，

∵BC=18，=12，

∴；

（2）∵四边形EFGH是矩形，

∴∠KEH=∠EHD=90°，

又∵∠EKD=90°，

∴四边形EHDK是矩形，

∴KD=EH=x，

∴，

∵，

∴，

∴，

当时，有最大值为54．