ЬтФПФкШн
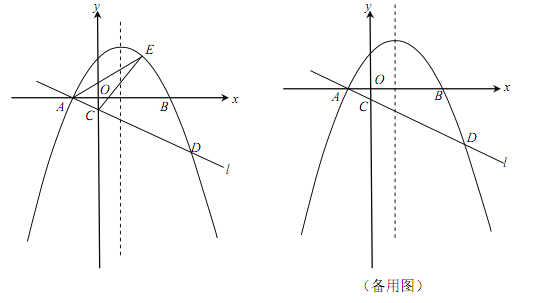
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж12ЗжЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯп![]() ЃЈ
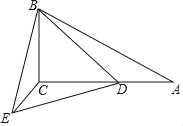
ЃЈ![]() ЃЉгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌОЙ§ЕуAЕФжБЯпlЃК
ЃЉгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌОЙ§ЕуAЕФжБЯпlЃК![]() гыyжсИКАыжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊDЃЌЧвCD=4ACЃЎ
гыyжсИКАыжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊDЃЌЧвCD=4ACЃЎ
ЃЈ1ЃЉжБНгаДГіЕуAЕФзјБъЃЌВЂЧѓжБЯпlЕФКЏЪ§БэДяЪНЃЈЦфжаkЃЌbгУКЌaЕФЪНзгБэЪОЃЉЃЛ
ЃЈ2ЃЉЕуEЪЧжБЯпlЩЯЗНЕФХзЮяЯпЩЯЕФЖЏЕуЃЌШєЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЧѓaЕФжЕЃЛ
ЃЌЧѓaЕФжЕЃЛ
ЃЈ3ЃЉЩшPЪЧХзЮяЯпЕФЖдГЦжсЩЯЕФвЛЕуЃЌЕуQдкХзЮяЯпЩЯЃЌвдЕуAЃЌDЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮФмЗёГЩЮЊОиаЮЃПШєФмЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈЃ1ЃЌ0ЃЉЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉPЕФзјБъЮЊЃЈ1ЃЌ
ЃЛЃЈ3ЃЉPЕФзјБъЮЊЃЈ1ЃЌ![]() ЃЉЛђЃЈ1ЃЌЃ4ЃЉЃЎ
ЃЉЛђЃЈ1ЃЌЃ4ЃЉЃЎ
ЁОНтЮіЁП
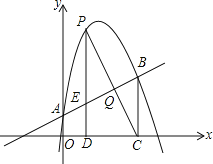
ЪдЬтЃЈ1ЃЉдк![]() жаЃЌСюy=0ЃЌЕУЕН
жаЃЌСюy=0ЃЌЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌЕУЕНAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгЩжБЯпlОЙ§ЕуAЃЌЕУЕН
ЃЌЕУЕНAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгЩжБЯпlОЙ§ЕуAЃЌЕУЕН![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌСю
ЃЌСю![]() ЃЌМД
ЃЌМД![]() ЃЌгЩгкCDЃН4ACЃЌЙЪЕуDЕФКсзјБъЮЊ4ЃЌМДга
ЃЌгЩгкCDЃН4ACЃЌЙЪЕуDЕФКсзјБъЮЊ4ЃЌМДга![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌДгЖјЕУГіжБЯпlЕФКЏЪ§БэДяЪНЃЛ
ЃЌДгЖјЕУГіжБЯпlЕФКЏЪ§БэДяЪНЃЛ
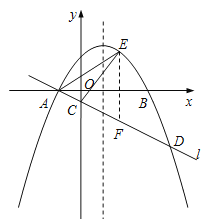
ЃЈ2ЃЉЙ§ЕуEзїEFЁЮyжсЃЌНЛжБЯпlгкЕуFЃЌЩшEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдђFЃЈ
ЃЉЃЌдђFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
EFЃН![]() =
=![]() ЃЌSЁїACEЃНSЁїAFEЃSЁїCFEЃН
ЃЌSЁїACEЃНSЁїAFEЃSЁїCFEЃН![]() ЃН
ЃН![]() ЃЌЙЪЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЙЪЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЖјЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЖјЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСю![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЕУЕНDЃЈ4ЃЌ5aЃЉЃЌвђЮЊХзЮяЯпЕФЖдГЦжсЮЊ
ЃЌЕУЕНDЃЈ4ЃЌ5aЃЉЃЌвђЮЊХзЮяЯпЕФЖдГЦжсЮЊ![]() ЃЌЩшPЃЈ1ЃЌmЃЉЃЌШЛКѓЗжСНжжЧщПіЬжТлЃКЂйШєADЪЧОиаЮЕФвЛЬѕБпЃЌЂкШєADЪЧОиаЮЕФвЛЬѕЖдНЧЯпЃЎ
ЃЌЩшPЃЈ1ЃЌmЃЉЃЌШЛКѓЗжСНжжЧщПіЬжТлЃКЂйШєADЪЧОиаЮЕФвЛЬѕБпЃЌЂкШєADЪЧОиаЮЕФвЛЬѕЖдНЧЯпЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁп![]() =
=![]() ЃЌСюy=0ЃЌЕУЕН
ЃЌСюy=0ЃЌЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌЁрAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌЁпжБЯпlОЙ§ЕуAЃЌЁр
ЃЌЁрAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌЁпжБЯпlОЙ§ЕуAЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЌЁр
ЃЌЁр![]() ЃЌСю
ЃЌСю![]() ЃЌМД
ЃЌМД![]() ЃЌЁпCDЃН4ACЃЌЁрЕуDЕФКсзјБъЮЊ4ЃЌЁр
ЃЌЁпCDЃН4ACЃЌЁрЕуDЕФКсзјБъЮЊ4ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁржБЯпlЕФКЏЪ§БэДяЪНЮЊ
ЃЌЁржБЯпlЕФКЏЪ§БэДяЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуEзїEFЁЮyжсЃЌНЛжБЯпlгкЕуFЃЌЩшEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдђFЃЈ
ЃЉЃЌдђFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
EFЃН![]() =
=![]() ЃЌ
ЃЌ
SЁїACEЃНSЁїAFEЃSЁїCFEЃН![]()
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЁпЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЁпЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЁр
ЃЌЁр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСю![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЁрDЃЈ4ЃЌ5aЃЉЃЌЁп
ЃЌЁрDЃЈ4ЃЌ5aЃЉЃЌЁп![]() ЃЌЁрХзЮяЯпЕФЖдГЦжсЮЊ
ЃЌЁрХзЮяЯпЕФЖдГЦжсЮЊ![]() ЃЌЩшPЃЈ1ЃЌmЃЉЃЌ
ЃЌЩшPЃЈ1ЃЌmЃЉЃЌ
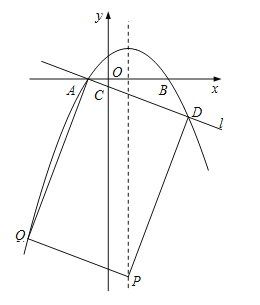
ЂйШєADЪЧОиаЮЕФвЛЬѕБпЃЌдђQЃЈЃ4ЃЌ21aЃЉЃЌmЃН21aЃЋ5aЃН26aЃЌдђPЃЈ1ЃЌ26aЃЉЃЌЁпЫФБпаЮADPQЮЊОиаЮЃЌЁрЁЯADPЃН90ЁуЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌМД
ЃЌМД![]() ЃЌЁп
ЃЌЁп![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁрP1ЃЈ1ЃЌ
ЃЌЁрP1ЃЈ1ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
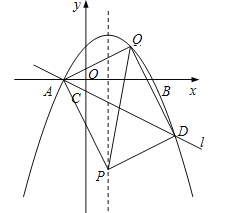
ЂкШєADЪЧОиаЮЕФвЛЬѕЖдНЧЯпЃЌдђЯпЖЮADЕФжаЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌQЃЈ2ЃЌ
ЃЉЃЌQЃЈ2ЃЌ![]() ЃЉЃЌmЃН
ЃЉЃЌmЃН![]() ЃЌдђPЃЈ1ЃЌ8aЃЉЃЌЁпЫФБпаЮAPDQЮЊОиаЮЃЌЁрЁЯAPDЃН90ЁуЃЌЁр
ЃЌдђPЃЈ1ЃЌ8aЃЉЃЌЁпЫФБпаЮAPDQЮЊОиаЮЃЌЁрЁЯAPDЃН90ЁуЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌМД
ЃЌМД![]() ЃЌЁп
ЃЌЁп![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁрP2ЃЈ1ЃЌЃ4ЃЉЃЎ
ЃЌЁрP2ЃЈ1ЃЌЃ4ЃЉЃЎ
злЩЯЫљЪіЃЌвдЕуAЁЂDЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮФмГЩЮЊОиаЮЃЌЕуPЕФзјБъЮЊЃЈ1ЃЌ![]() ЃЉЛђЃЈ1ЃЌЃ4ЃЉЃЎ
ЃЉЛђЃЈ1ЃЌЃ4ЃЉЃЎ

 УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ
УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ