题目内容
【题目】如图1,ABCD中,∠ABC、∠ADC的平分线分别交AD、BC于点E、F.
(1)求证:四边形EBFD是平行四边形;
(2)如图2,小明在完成(1)的证明后继续进行了探索.连接AF、CE,分别交BE、FD于点G、H,得到四边形EGFH.此时,他猜想四边形EGFH是平行四边形,请在框图(图3)中补全他的证明思路,再在答题纸上写出规范的证明过程.
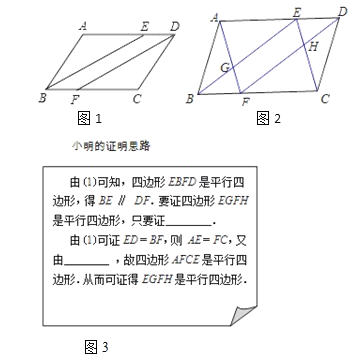
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)由平行四边形的性质得出AD∥BC,∠ABC=∠ADC.AD=BC,由角平分线得出∠ABE=∠EBC=∠ADF=∠CDF.证出EB∥DF,即可得出结论;
(2)由平行四边形的性质得出BE∥DF,DE=BF,得出AE=CF,证出四边形AFCE是平行四边形,得出GF∥EH,即可证出四边形EGFH是平行四边形.
证明:在![]() ABCD 中,AD∥BC,∠ABC=∠ADC.AD=BC.
ABCD 中,AD∥BC,∠ABC=∠ADC.AD=BC.
∵BE 平分∠ABC,∴∠ABE=∠EBC=![]() ∠ABC.
∠ABC.
∵DF 平分∠ADC,∴∠ADF=∠CDF=![]() ∠ADC.
∠ADC.
∵∠ABC=∠ADC.
∴∠ABE=∠EBC=∠ADF=∠CDF.
∵AD∥BC,
∴∠AEB=∠EBC.
∴∠AEB=∠ADF.
∴EB∥DF.
∵ED∥BF,
∴四边形 EBFD 是平行四边形.
(2)①补全思路:GF∥EH,AE∥CF;
②理由如下:
∵四边形 EBFD 是平行四边形;
∴BE∥DF,DE=BF,
∴AE=CF,
又∵AE∥CF,
∴四边形 AFCE 是平行四边形,
∴GF∥EH,
∴四边形 EGFH 是平行四边形.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目