题目内容
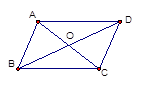
如图,在四边形 中,点
中,点 ,
, 分别是
分别是 的中点,
的中点, 分别是
分别是 的中点,
的中点, 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?请证明你的结论.
是菱形?请证明你的结论.
 中,点
中,点 ,
, 分别是
分别是 的中点,
的中点, 分别是
分别是 的中点,
的中点, 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?请证明你的结论.
是菱形?请证明你的结论.
当 时,四边形
时,四边形 是菱形。证明见解析
是菱形。证明见解析
 时,四边形
时,四边形 是菱形。证明见解析
是菱形。证明见解析(1)当 时,四边形
时,四边形 是菱形.·············· 1分
是菱形.·············· 1分
(2)证明: 点
点 分别是
分别是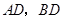 的中点,
的中点,
 ,同理
,同理 ,
, .
.
 四边形
四边形 是平行四边形························ 6分
是平行四边形························ 6分
 ,又可同理证得
,又可同理证得 ,
,
 ,
,
 ,
,
 四边形
四边形 是菱形.·························· 9分
是菱形.·························· 9分
(用分析法由四边形 是菱形推出满足条件“
是菱形推出满足条件“ ”也对)
”也对)
根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥=HF.
因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH= CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件
 时,四边形
时,四边形 是菱形.·············· 1分
是菱形.·············· 1分(2)证明:
 点
点 分别是
分别是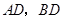 的中点,
的中点, ,同理
,同理 ,
, .
. 四边形
四边形 是平行四边形························ 6分
是平行四边形························ 6分 ,又可同理证得
,又可同理证得 ,
, ,
, ,
, 四边形
四边形 是菱形.·························· 9分
是菱形.·························· 9分(用分析法由四边形
 是菱形推出满足条件“
是菱形推出满足条件“ ”也对)
”也对)根据菱形的定义来求解.E、G分别是AD,BD的中点,那么EG就是三角形ADB的中位线,同理,HF是三角形ABC的中位线,因此EG、HF同时平行且相等于AB,因此EG∥=HF.
因此四边形EHFG是平行四边形,E、H是AD,AC的中点,那么EH=
 CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件
CD,要想证明EHFG是菱形,那么就需证明EG=EH,那么就需要AB、CD满足AB=CD的条件
练习册系列答案
相关题目
 中,
中, ,
, ,点
,点 是边
是边 上的动点(点
上的动点(点 ,点
,点 重合),过点
重合),过点 ,交
,交 边于
边于 点,再把
点,再把 沿着动直线
沿着动直线 对折,点
对折,点 点,设
点,设 的长度为
的长度为 ,
, 与矩形
与矩形 .
. 的度数;
的度数; 边上?
边上? ?
?
 是等边三角形,点E在正方形
是等边三角形,点E在正方形 内,在对角线AC上有一点P,使
内,在对角线AC上有一点P,使 的和最小,则这个最小值为( )
的和最小,则这个最小值为( )


 中,
中, ∥
∥ ,
, ,
, 交
交 于点
于点 ,点
,点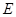 、
、 分别为
分别为 、
、 的中点,则下列关于点
的中点,则下列关于点




 ,
,
 中,
中,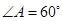 ,对角线
,对角线 ,则菱形
,则菱形
 中,
中, 是
是 边上的一点,
边上的一点, 是
是 的中点,过点
的中点,过点 作
作 的延长线于
的延长线于 ,且
,且 ,连结
,连结 .
. ,试猜测四边形
,试猜测四边形 的形状,并证明你的结论.
的形状,并证明你的结论.
 是
是 的中点,且
的中点,且 ,有下列结论:①.两三角形面积
,有下列结论:①.两三角形面积 ②.
②. ③.四边形
③.四边形 是等腰梯形 ④.
是等腰梯形 ④. 其中不正确的是_________________.
其中不正确的是_________________.
