题目内容
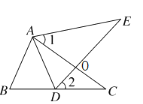
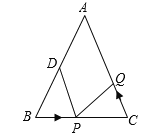
【题目】如图 1,将两个完全相同的三角形纸片 ABC 和 DEC重合放置,其中∠C=90°,∠B=∠E=30°.
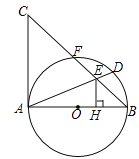
(1)如图2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落 在 AB 边上时,
①填空:线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,求证:S1=S2

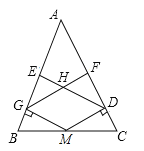
(2)当△DEC 绕点 C 旋转到如图 3 所示的位置时,小明猜想(1) 中 S1 与 S2 的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE 边上的高,请你证明小明的猜想.
【答案】(1)DE∥AC,
②S1=S2.
(2)答案见详解.
【解析】
(1)利用旋转可知![]() ,根据
,根据![]() ,得出
,得出![]() 是等边三角形,所以
是等边三角形,所以![]() ,证得
,证得![]() ,
,
②由图得知![]() 和
和![]() 同高,
同高,![]() 和
和![]() 同高,利用三角形面积公式,得到
同高,利用三角形面积公式,得到![]() .
.
(2)由图形是旋转得到,利用![]() 可以证明
可以证明![]() ,所以
,所以![]() ,利用三角形面积公式可以求证.
,利用三角形面积公式可以求证.
解: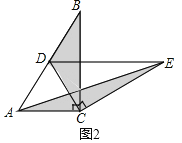
(1)①如图2中,
由旋转可知:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
②∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
即:![]() .
.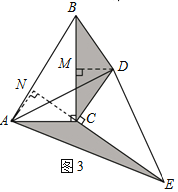
(2)如图3中,
∵![]() 是由
是由![]() 绕点
绕点![]() 旋转得到,
旋转得到,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,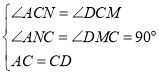 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目