Question

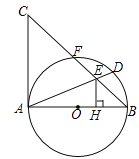
【题目】如图，已知AB为⊙O直径，AC是⊙O的切线，连接BC交⊙O于点F，取的中点D，连接AD交BC于点E，过点E作EH⊥AB于H．

（1）求证：△HBE∽△ABC；

（2）若CF=4，BF=5，求AC和EH的长．

Answer 1

【答案】（1）证明见解析；（2）CA=6，EH=2．

【解析】（1）根据切线的性质即可证明：∠CAB=∠EHB，由此即可解决问题；

（2）连接AF．由△CAF∽△CBA，推出CA2=CFCB=36，推出CA=6，AB=，AF=，由Rt△AEF≌Rt△AEH，推出AF=AH=2，设EF=EH=x．在Rt△EHB中，可得（5﹣x）2=x2+（）2，解方程即可解决问题；

（1）∵AC是⊙O的切线，

∴CA⊥AB．

∵EH⊥AB，

∴∠EHB=∠CAB．

∵∠EBH=∠CBA，

∴△HBE∽△ABC．

（2）连接AF．

∵AB是直径，

∴∠AFB=90°．

∵∠C=∠C，∠CAB=∠AFC，

∴△CAF∽△CBA，

∴CA2=CFCB=36，

∴CA=6，AB=，AF=．

∵，

∴∠EAF=∠EAH．

∵EF⊥AF，EH⊥AB，

∴EF=EH．

∵AE=AE，

∴Rt△AEF≌Rt△AEH，

∴AF=AH=2.

设EF=EH=x．在Rt△EHB中，（5﹣x）2=x2+（）2，

∴x=2，

∴EH=2．