题目内容
如图a,梯形ABCD中,AB∥CD,AB=a,CD=b,点E、F分别是两腰AD、BC上的点,且EF∥AB,设EF到CD、AB的距离分别为d1、d2,某同学在对这一图形进行研究时,发现如下事实:①当
| d1 |
| d2 |
| 1 |
| 1 |
| a+b |
| 2 |
当
| d1 |
| d2 |
| 1 |
| 2 |
| a+2b |
| 3 |
当
| d1 |
| d2 |
| 1 |
| 3 |
| a+3b |
| 4 |
当
| d1 |
| d2 |
| 1 |
| 4 |
| a+4b |
| 5 |
②当
| d1 |
| d2 |
| 2 |
| 1 |
| 2a+b |
| 3 |
| d1 |
| d2 |
| 3 |
| 1 |
| 3a+b |
| 4 |
当
| d1 |
| d2 |
| 4 |
| 1 |
| 4a+b |
| 5 |
| d1 |
| d2 |
| 5 |
| 1 |
| 5a+b |
| 6 |
根据以上结论,解答下列问题:
(1)猜想当
| d1 |
| d2 |
| 1 |
| n |
| d1 |
| d2 |
| m |
| 1 |
(2)进一步猜想当
| d1 |
| d2 |
| m |
| n |
(3)如图b,有一块梯形耕地ABCD,AB∥CD,CD=100米,AB=300米,AD=500米,在AD上取两点E、F,使DE=200米,EF=150米,分别从E、F两处为起点开挖两条平行于两底的水渠,直到另一腰,求这两条水渠的总长度.
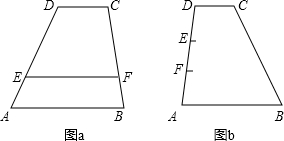
分析:(1)由题中已知条件,不难得出规律,即当
=
时,EF=
;当
=
时,EF=
;
(2)猜想,还需进行验证,可延长AD、BC交于G,设△DCG在BC边上的高为h,再利用相似三角形对应边成比例,进而可得结论.
(3)对(2)结论的实际运用,由(2)中结论可得两条水渠的总长度.
| d1 |
| d2 |
| 1 |
| n |
| a+nb |
| n+1 |
| d1 |
| d2 |
| m |
| 1 |
| ma+b |
| m+1 |
(2)猜想,还需进行验证,可延长AD、BC交于G,设△DCG在BC边上的高为h,再利用相似三角形对应边成比例,进而可得结论.
(3)对(2)结论的实际运用,由(2)中结论可得两条水渠的总长度.
解答: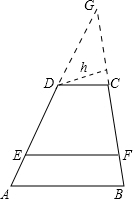 解:(1)当
解:(1)当
=
时,EF=
;
当
=
时,EF=
.
(2)当
=
时,EF=
.
证明:延长AD、BC交于G,设△DCG在BC边上的高为h,则由三角形相似得:
从上述关于h,EF的方程组中易求得EF=
.
(3)由于过点E平行于两底的水渠到两底的距离比等于2:3,由(2)中的结论可得:
水渠长=
=180(米)
由于过点F平行于两底的水渠到两底的距离比等于7:3,由(2)中的结论可得:
水渠长=
=240(米)
故两条水渠的总长度是180+240=420(米).
 解:(1)当
解:(1)当| d1 |
| d2 |
| 1 |
| n |
| a+nb |
| n+1 |
当
| d1 |
| d2 |
| m |
| 1 |
| ma+b |
| m+1 |
(2)当
| d1 |
| d2 |
| m |
| n |
| ma+nb |
| m+n |
证明:延长AD、BC交于G,设△DCG在BC边上的高为h,则由三角形相似得:
|
| ma+nb |
| m+n |
(3)由于过点E平行于两底的水渠到两底的距离比等于2:3,由(2)中的结论可得:
水渠长=
| 2BC+3AD |
| 2+3 |
由于过点F平行于两底的水渠到两底的距离比等于7:3,由(2)中的结论可得:
水渠长=
| 7BC+3AD |
| 7+3 |
故两条水渠的总长度是180+240=420(米).
点评:能够求解一些简单的规律性问题,能够将数学知识熟练地运用到实际生活当中.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数.
如图,在梯形ABCD中,AD∥BC,AB=DC=AD,AC=BC,求∠ACB的度数. 如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形?
如图,在梯形ABCD中,AD∥BC,BC=30cm,动点M从A点开始沿AD边向D以1cm/s的速度运动,动点N从C点开始沿CB边向B以3cm/s的速度运动,M、N分别从A、C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t s,t为何值时,四边形ABNM是平行四边形? 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ACB=40°,∠ACD=30°,则∠B=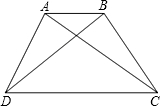 如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积.
如图,在梯形ABCD中,AB∥CD,AD=BC,AC⊥BD,AB+CD=20,求梯形ABCD的面积. 如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=
如图,等腰梯形ABCD中,AD=2,BC=6,高DF=2,则腰长DC=