题目内容
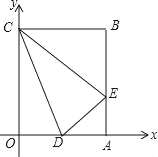
【题目】矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D的坐标为(2,0),E为AB上的点,当△CDE的周长最小时,点E的坐标为( )
A. (1,3) B. (3,1) C. (4,1) D. (3,2)
【答案】B
【解析】
作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,先求出直线CH解析式,再求出直线CH与AB的交点即可解决问题.
作点D关于直线AB的对称点H,连接CH与AB的交点为E,此时△CDE的周长最小,如图所示:

∵D(2,0),A(3,0),
∴H(4,0),
设直线CH解析式为y=ax+b,则:
![]() ,解得:
,解得:![]() ,
,
所以直线CH解析式为y=-x+4,
∴x=3时,y=-3+4=1,
∴点E坐标(3,1)
故选:B.

练习册系列答案
相关题目