题目内容
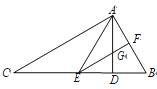
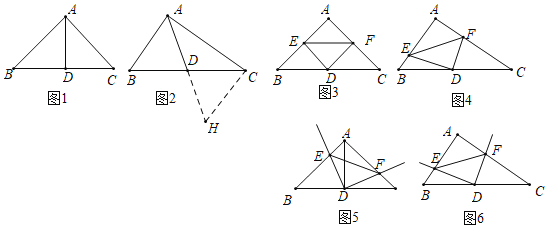
【题目】如图,AC平分钝角∠BAE交过B点的直线于点C,BD平分∠ABC交AC于点D,且∠BAD+∠ABD=90°.
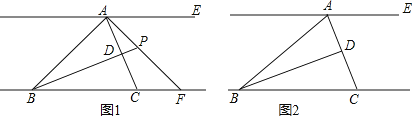
(1)求证:AE∥BC;
(2)点F是射线BC上一动点(点F不与点B,C重合),连接AF,与射线BD相交于点P.
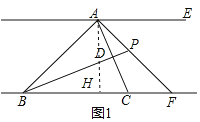
(ⅰ)如图1,若∠ABC=45°,AF⊥AB,试探究线段BF与CF之间满足的数量关系;
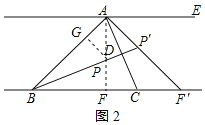
(ⅱ)如图2,若AB=10,S△ABC=30,∠CAF=∠ABD,求线段BP的长.
【答案】(1)见解析;(2)(ⅰ)BF=(2+![]() )CF;理由见解析;(ⅱ)BP=
)CF;理由见解析;(ⅱ)BP=![]() .
.
【解析】
(1)先求出∠BAE+∠ABC=180°,再根据同旁内角互补两直线平行,即可证明AE∥BC.
(2)(ⅰ)过点A作AH⊥BC于H,如图1所示,先证明△ABH、△BAF是等腰直角三角形,再根据等腰直角三角形的性质,求证BF=(2+![]() )CF即可.
)CF即可.
(ⅱ)①当点F在点C的左侧时,作PG⊥AB于G,如图2所示,先通过三角形面积公式求出AF的长,再根据勾股定理求得BF、AC、BD的长,证明Rt△BPG≌Rt△BPF(HL),以此得到AD的长,设AP=x,则PG=PF=6﹣x,利用勾股定理求出AP的长,再利用勾股定理求出PD的长,通过BP=BD﹣PD即可求出线段BP的长.
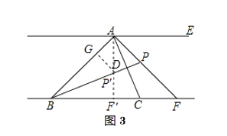
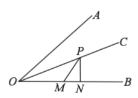
②当点F在点C的右侧时,则∠CAF=∠ACF',P’和F’分别对应图2中的P和F,如图3所示,根据等腰三角形的性质求得PD=P'D=![]() ,再根据①中的结论,可得BP=BP'+ P'P=
,再根据①中的结论,可得BP=BP'+ P'P=![]() .
.
(1)∵AC平分钝角∠BAE,BD平分∠ABC,
∴∠BAE=2∠BAD,∠ABC=2∠ABD,
∴∠BAE+∠ABC=2(∠BAD+∠ABD)=2×90°=180°,
∴AE∥BC;
(2)解:(ⅰ)BF=(2+![]() )CF;理由如下:
)CF;理由如下:
∵∠BAD+∠ABD=90°,
∴BD⊥AC,
∴∠CBD+∠BCD=90°,
∵∠ABD=∠CBD,
∴∠BAD=∠BCD,
∴AB=BC,
过点A作AH⊥BC于H,如图1所示:
∵∠ABC=45°,AF⊥AB,
∴△ABH、△BAF是等腰直角三角形,
∴AH=BH=HF,BC=AB=![]() BH,BF=
BH,BF=![]() AB=
AB=![]() ×
×![]() BH=2BH,
BH=2BH,
∴CF=BF﹣BC=2BH﹣![]() BH=(2﹣
BH=(2﹣![]() )BH,
)BH,
∴BH=![]() =(1+
=(1+![]() )CF,
)CF,
∴BF=2(1+![]() )CF=(2+
)CF=(2+![]() )CF;
)CF;
(ⅱ)①当点F在点C的左侧时,如图2所示:
同(ⅰ)得:∠BAD=∠BCD,
∴AB=BC=10,
∵∠CAF=∠ABD,∠BAD+∠ABD=90°,
∴∠BCD+∠CAF=90°,
∴∠AFC=90°,
∴AF⊥BC,
则S△ABC=![]() BCAF=
BCAF=![]() ×10×AF=30,
×10×AF=30,
∴AF=6,
∴BF=![]() =8,
=8,
∴CF=BC﹣BF=10﹣8=2,
∴AC=![]() =2
=2![]() ,
,
∵S△ABC=![]() ACBD=
ACBD=![]() ×2
×2![]() ×BD=30,
×BD=30,
∴BD=3![]() ,
,
作PG⊥AB于G,则PG=PF,
在Rt△BPG和Rt△BPF中,
![]() ,
,
∴Rt△BPG≌Rt△BPF(HL),
∴BG=BF=8,
∴AG=AB﹣BG=2,
∵AB=CB,BD⊥AC,
∴AD=CD=![]() AC=
AC=![]() ,
,
设AP=x,则PG=PF=6﹣x,
在Rt△APG中,由勾股定理得:22+(6﹣x)2=x2,
解得:x=![]() ,
,
∴AP=![]() ,
,
∴PD=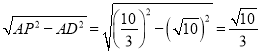 ,
,
∴BP=BD﹣PD=![]() ;
;
②当点F在点C的右侧时,P’和F’分别对应图2中的P和F,如图3所示 ,则∠CAF=∠CAF',
∵BD⊥AC,
∴![]()
∴∠APD=∠AP'D,
∴△![]() 是等腰三角形
是等腰三角形
∴AP=AP',PD=P'D=![]() ,
,
∴BP=BP'+ P'P=![]() ;
;
综上所述,线段BP的长为![]() 或
或![]() .
.