题目内容
【题目】如图,已知直线y=k1x+b与x轴、y轴相交于C、D两点,与y=![]() 交于A(m,2)、B(﹣2,n)两点.
交于A(m,2)、B(﹣2,n)两点.
(1)求m+n的值;
(2)连接OA、OB,若tan∠AOD+tan∠BOC=1.
①当不等式k1x+b>![]() 时,请结合图象求x的取值范围;
时,请结合图象求x的取值范围;
②设点E在y轴上,且满足∠AEO+∠AOD=45°,求点E的坐标.
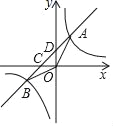
【答案】(1)m+n=0;(2) ①x>1或﹣2<x<0;②(0,5)或(0,﹣1).
【解析】
(1)利用点A,B在反比例函数上,代入反比例函数解析式中即可得出结论;
(2)①先表示出tan∠AOD和tan∠BOC,进而用tan∠AOD+tan∠BOC=1,建立方程借助m+n=0,求出m,n即可得出点A,B坐标,最后利用图象即可得出结论;
②分两种情况,
Ⅰ、当点E在AM上方时,先求出AO=![]() =
=![]() ,再判断出△AOM∽△E1ON,即可求出m的值.最后利用勾股定理求出OE1即可得出结论;
,再判断出△AOM∽△E1ON,即可求出m的值.最后利用勾股定理求出OE1即可得出结论;
Ⅱ、当点E在AM下方时,利用对称性即可得出结论.
解:∵点A(m,2),B(﹣2,n)在反比例函数y=![]() ,
,
∴k2=2m,k2=﹣2n,
∴2m+2n=0,
∴m+n=0;
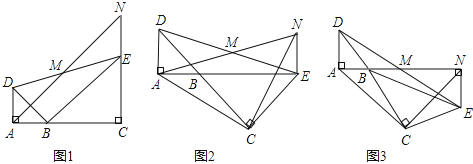
(2)①如图1,过点A作AM⊥y轴于M,过点B作BF⊥x轴于F,
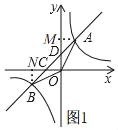
在Rt△AOM中,tan∠AOM=![]() =
=![]() ,
,
在Rt△BOF中,tan∠BOF=![]() =
=![]() =﹣
=﹣![]() ,
,
∵tan∠AOD+tan∠BOC=1,
∴![]() +(﹣
+(﹣![]() )=1,
)=1,
∴m﹣n=2,
∵m+n=0,
∴m=1,n=﹣1,
∴A(1,2),B(﹣2,﹣1),
∵k1x+b>![]() ,
,
∴y1>y2,
∴当x>1或﹣2<x<0时,k1x+b>![]() ;
;
②如图2,Ⅰ、当点E在AM上方时,过点E1作E1N⊥OA交OA的延长线于N,
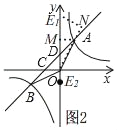
由题意知,∠E1AN=45°,
∴∠E1AN=∠AE1N=45°,
∴E1N=AN,
在Rt△OAM中,AM=1,OM=2,
∴AO=![]() =
=![]() ,
,
设E1N=AN=m,
∴ON=OA+AN=![]() +m,
+m,
∵∠AOM=∠E1ON,∠AMO=∠E1NO,
∴△AOM∽△E1ON,
∴![]() ,
,
∴![]() ,
,
∴m=![]() ,由勾股定理得,E1A=
,由勾股定理得,E1A=![]() ,E1M=3,
,E1M=3,
∴OE1=5,
∴E1(0,5);
Ⅱ、当点E在AM下方时,由对称性得,E2M=E1M=3,
∴OE2=1,
∴E2(0,﹣1),
综合可知,点E的坐标为(0,5)或(0,﹣1).

 阅读快车系列答案
阅读快车系列答案