题目内容
【题目】已知：点
在直线
上，点
都在直线
上（点
在点
的左侧），连接
，
平分
且
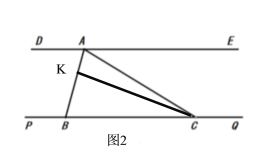
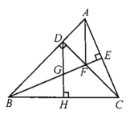
（1）如图1，求证： 
（2）如图2，点
为上一点，连接
，若
，求
的度数
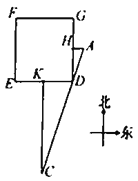
（3）在（2）的条件下，点
在直线上，连接
，且
，若
，求
的度数（要求：在备用图中画出图形后，再计算）
【答案】（1）见解析；（2）90°；（3）图形见解析，
或
【解析】
（1）根据角平分线的定义和已知条件可等量代换出∠DAB=∠ABC，即可判断；
（2）根据平行线的性质可等量代换得
，根据平行线的性质可得
，可等量代换得
，再根据三角形的内角和定理求解即可；
（3）分点
在点
的右侧，点在点左侧两种情况解答．
（1）
平分
又
（2）由（1）得：
∵
平分
∴
（3）
情况一：如图 ，点在点的右侧，过点
作，
，
，
， 
，
∴
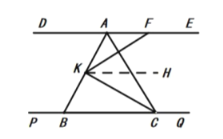
情况二：如图 ，点在点左侧，过点作
，
，
，，
设
，
则
，
，
，
，
解得
综上所述
的度数为 或
练习册系列答案
相关题目
【题目】某商场购进了一批
、
两种型号的智能扫地机器人，这两种智能扫地机器人的进购数量、进价、售价如表所示：
类型 | 进购数量（个） | 进价（元/个） | 售价（元/个） |
| 20 | 1800 | 2300 |
| 40 | 1500 | ？ |
若该商场计划全部销售完这批智能扫地机器人的总利润不少于32000元，则型智能扫地机器人的销售单价至少是多少元？
