题目内容
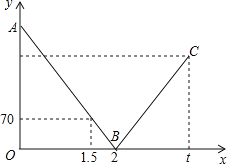
【题目】一辆快车从甲地驶往乙地，一辆慢车从乙地驶往甲地，两车同时出发，匀速行驶．设行驶的时间为x（时），两车之间的距离为y（千米），如图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系．已知两车相遇时快车比慢车多行驶40千米，若快车从甲地到达乙地所需时间为t时，则t的值为_____．
【答案】3.5
【解析】
设线段AB所在直线的函数关系式为y＝kx+b，待定系数法求出AB所在直线解析式，当x＝0时，即为甲、乙两地距离，求出y＝280，设快车的速度为每小时m千米，慢车的速度为每小时n千米，利用两车行驶距离得出等式方程求出即可．
解：设线段AB所在直线的函数关系式为y＝kx+b，
把（1.5，70）、（2，0）代入得；
，
解得：
，
∴y＝﹣140x+280
∴x＝0时，y＝280，即甲、乙两地间的距离为280千米，
设快车的速度为每小时m千米，慢车的速度为每小时n千米，
由题意得，
，
解得：
，
∴t＝
＝3.5，
故答案为：3.5．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
