��Ŀ����
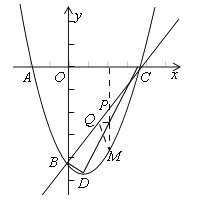
����Ŀ����֪��m��n��һԪ���η���x2+4x+3=0������ʵ��������|m|��|n|��������y=x2+bx+c��ͼ����A��m��0����B��0��n������ͼ��ʾ��
��1������������ߵĽ���ʽ��
��2���裨1���е���������x�����һ������Ϊ�����ߵĶ���ΪD�������C��D�����꣬���ж���BCD����״��
��3����P��ֱ��BC�ϵ�һ�����㣨��P�����B�͵�C�غϣ�������P��x��Ĵ��ߣ����������ڵ�M����Q��ֱ��BC�ϣ������PΪ![]() ����λ���ȣ����P�ĺ�����Ϊt����PMQ�����ΪS�����S��t֮��ĺ�����ϵʽ��
����λ���ȣ����P�ĺ�����Ϊt����PMQ�����ΪS�����S��t֮��ĺ�����ϵʽ��

���𰸡���1��![]() ����2��C��3��0����D��1����4������BCD��ֱ������������3��
����2��C��3��0����D��1����4������BCD��ֱ������������3��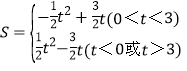
��������
���⣨1���Ƚ�һԪ���η��̣�Ȼ���ô���ϵ������������߽���ʽ��
��2���Ƚⷽ�������������x��Ľ��㣬���жϳ���BOC����BED���ǵ���ֱ�������Σ��Ӷ��õ����ۣ�
��3�������QF=1���ٷ��������������P�ڵ�M�Ϸ����·����ֱ���㼴�ɣ�
����������⣨1����![]() ����
����![]() ��
��![]() ����m��n��һԪ���η���
����m��n��һԪ���η���![]() ������ʵ��������|m|��|n|����m=��1��n=��3����������
������ʵ��������|m|��|n|����m=��1��n=��3����������![]() ��ͼ����A��m��0����B��0��n������
��ͼ����A��m��0����B��0��n������![]() ����
����![]() ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2����y=0����![]() ����
����![]() ��
��![]() ����C��3��0������
����C��3��0������![]() =
=![]() ������������D��1����4��������D��DE��y�ᣬ��OB=OC=3����BE=DE=1�����BOC����BED���ǵ���ֱ�������Σ����OBC=��DBE=45�������CBD=90�������BCD��ֱ�������Σ�
������������D��1����4��������D��DE��y�ᣬ��OB=OC=3����BE=DE=1�����BOC����BED���ǵ���ֱ�������Σ����OBC=��DBE=45�������CBD=90�������BCD��ֱ�������Σ�
��3����ͼ����B��0����3����C��3��0������ֱ��BC����ʽΪy=x��3������P�ĺ�����Ϊt��PM��x�ᣬ����M�ĺ�����Ϊt������P��ֱ��BC�ϣ���M���������ϣ���P��t��t��3����M��t��![]() ��������Q��QF��PM�����PQF�ǵ���ֱ�������Σ���PQ=
��������Q��QF��PM�����PQF�ǵ���ֱ�������Σ���PQ=![]() ����QF=1��
����QF=1��
������P�ڵ�M�Ϸ�ʱ����0��t��3ʱ��PM=t��3����![]() ��=
��=![]() ����S=
����S=![]() PM��QF=
PM��QF=![]() =
=![]() ������ͼ3������P�ڵ�M�·�ʱ����t��0��t��3ʱ��PM=
������ͼ3������P�ڵ�M�·�ʱ����t��0��t��3ʱ��PM=![]() ����t��3��=
����t��3��=![]() ����S=
����S=![]() PM��QF=
PM��QF=![]() ��
��![]() ��=
��=![]() ��
��
����������S=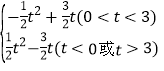 ��
��