题目内容
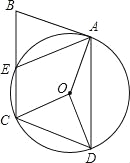
【题目】如图,ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,BC与⊙O交于点E,设∠OCD=α,∠BAD=β.
(1)求证:AB=AE;
(2)试探究α与β之间的数量关系.
【答案】(1)证明参见解析;(2)β=135°﹣![]() α.
α.
【解析】
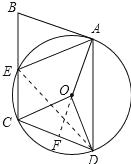
试题分析:(1)连接DE,先证明∠CED=∠ADE,推出弧AE=弧CD,进一步推出AE=CD,因为AB=CD,由此即可证明;(2)延长AO交CD于F,由β=90°+∠OAD,∠OAD=![]() ∠FOD,∠FOD=∠FOC=90°﹣α,由此即可解决问题.
∠FOD,∠FOD=∠FOC=90°﹣α,由此即可解决问题.
试题解析:(1)连接DE.先证明∠CED=∠ADE,∵四边形ABCD是平行四边形,∴BC∥AD,AB=CD,∴∠CED=∠ADE,∴弧AE=弧CD,∴AE=CD,∵AB=CD,∴AB=AE;(2)延长AO交CD于F,∵AB是⊙O切线,∴AB⊥AF,∵AB∥CD,∴AF⊥CD,∵OC=OD,∴∠OCD=∠ODC,∴∠COF=∠DOF=90°﹣α,∵∠OAD=∠ODA,∴![]() (90°﹣α),∴β=∠BAF+∠OAD=90°+∠OAD=90°+
(90°﹣α),∴β=∠BAF+∠OAD=90°+∠OAD=90°+![]() (90°﹣α)=135°﹣
(90°﹣α)=135°﹣![]() α.故α与β之间的数量关系为β=135°﹣
α.故α与β之间的数量关系为β=135°﹣![]() α.
α.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目