题目内容
【题目】已知在平面直角坐标系中，AB 两点的坐标分别为 A(1,4),B(5,1),P，Q 分别是 x 轴，y 轴 上两个动点，则四边形 ABPQ 的周长最小值为（ ）
A.5B.5 
C.
D.
【答案】D
【解析】
作点A关于y轴的对称点A'，点B关于x轴的对称点B'，连接A'B'，交x轴于P，交y轴于Q，连接AQ，BP，则四边形AQPB周长的最小值等于A'B'+AB，利用勾股定理进行计算，即可得到四边形AQPB周长的最小值．
解：如图所示，作点A关于y轴的对称点A'，点B关于x轴的对称点B'，连接A'B'，交x轴于P，交y轴于Q，连接AQ，BP，则四边形AQPB周长的最小值等于A'B'+AB，
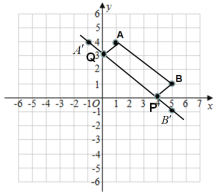
∵A（1，4），B（5，1），
∴A'（-1，4），B'（5，-1），
∴A'B'=
，
∴四边形AQPB周长的最小值等于
，
故选D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
