题目内容
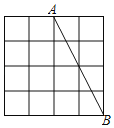
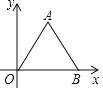
【题目】如图，等边△AOB中，点B在x轴正半轴上，点A坐标为（1， 
），将△AOB绕点O顺时针旋转15°，此时点A对应点A′的坐标是（ ）
A.（2，2）B.（，1）C.
D.（
,）
【答案】D
【解析】
作AE⊥OB于E，A′H⊥OB于H，根据A点坐标可以求出AO的长度，因△AOB是等边三角形，∠AOA′=15°，所以△OA′H是等腰直角三角形，AO=A′O，即可求解.
解：如图，作AE⊥OB于E，A′H⊥OB于H．
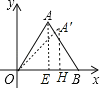
∵A（1，
），
∴OE＝1，AE＝，
∴OA＝
，
∵△OAB是等边三角形，
∴∠AOB＝60°，
∵∠AOA′＝15°，
∴∠A′OH＝60°﹣15°＝45°，
∵OA′＝OA＝2，A′H⊥OH，
∴A′H＝OH＝
，
∴A′（，），
故选：D．
练习册系列答案
相关题目
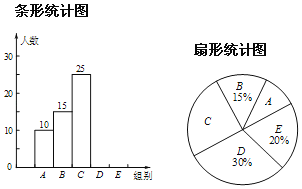
【题目】嘉善县将开展以“珍爱生命，铁拳护航”为主题的交通知识竞赛，某校对参加选拔赛的若干名同学的成绩按A，B，C，D四个等级进行统计，绘制成如下不完整的频数统计表和扇形统计图
成绩等级 | 频数（人数） | 频率 |
A | 4 | 0.08 |
B | m | 0.52 |
C | n | |
D | ||
合计 | 1 |
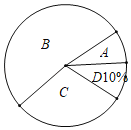
（1）求m＝ ，n＝ ；
（2）在扇形统计图中，求“C等级”所对应圆心角的度数；
（3）“A等级”的4名同学中有3名男生和1名女生，现从中随机挑选2名同学代表学校参加全县比赛，请用树状图法或列表法求出恰好选中“一男一女”的概率．
