题目内容
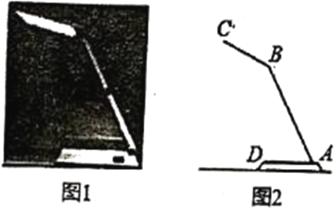
【题目】如图1是一种折叠台灯,将其放置在水平桌面上,图2是其简化示意图,测得其灯臂![]() 长为
长为![]() 灯翠
灯翠![]() 长为
长为![]() ,底座
,底座![]() 厚度为
厚度为![]() 根据使用习惯,灯臂
根据使用习惯,灯臂![]() 的倾斜角
的倾斜角![]() 固定为
固定为![]() ,
,
(1)当![]() 转动到与桌面平行时,求点
转动到与桌面平行时,求点![]() 到桌面的距离;
到桌面的距离;
(2)在使用过程中发现,当![]() 转到至
转到至![]() 时,光线效果最好,求此时灯罩顶端
时,光线效果最好,求此时灯罩顶端![]() 到桌面的高度(参考数据:
到桌面的高度(参考数据:![]() ,结果精确到个位).
,结果精确到个位).
【答案】(1)点![]() 到桌面的距离为
到桌面的距离为![]() ;(2)灯罩顶端
;(2)灯罩顶端![]() 到桌面的高度约为
到桌面的高度约为![]() .
.
【解析】
(1)作CM⊥EF于M,BP⊥AD于P,交EF于N,则CM=BN,PN=3,由直角三角形的性质得出AP=![]() AB=14,BP=
AB=14,BP=![]() AP=14
AP=14![]() ,得出CM=BN=BP+PN=14
,得出CM=BN=BP+PN=14![]() +3即可;
+3即可;
(2)作CM⊥EF于M,作BQ⊥CM于Q,BP⊥AD于P,交EF于N,则∠QBN=90°,CM=BN,PN=3,由(1)得QM=BN,求出∠CBQ=25![]() ,由三角函数得出CQ=BC×sin25
,由三角函数得出CQ=BC×sin25![]() ,得出CM=CQ+QM即可.
,得出CM=CQ+QM即可.
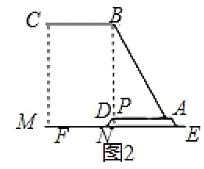
解![]() 当
当![]() 转动到与桌面平行时,
转动到与桌面平行时,
如图2所示:作![]() 于
于![]() 于
于![]() ,交
,交![]() 于
于![]() 则
则![]()
![]()
![]() ,
,![]()
![]()
即点![]() 到桌面的距离为
到桌面的距离为![]() ;
;
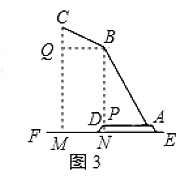
![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() 于
于![]() ,交
,交![]() 于
于![]() ,如图3所示:
,如图3所示:
则![]() ,
,
由![]() 得
得![]()
![]() ,
,
![]()
在![]() 中,
中,![]()
![]() ,
,
即此时灯罩顶端![]() 到桌面的高度约为
到桌面的高度约为![]() .
.

练习册系列答案
相关题目