题目内容
已知点A(-2,0),点B(0,2),点C在第二、四象限坐标轴夹角平分线上,∠BAC=60°,那么点C的坐标为分析:首先根据等腰三角形的性质得出CO垂直平分AB,进而求出△ABC是等边三角形,再利用勾股定理求出C到x轴的距离,即可得出C点坐标,同理可以求出所有符合要求的结果.
解答: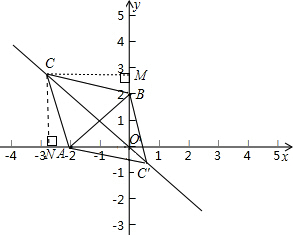 解:过点C作CM⊥y轴于点M,作CN⊥x轴于点N.
解:过点C作CM⊥y轴于点M,作CN⊥x轴于点N.
∵点A(-2,0),点B(0,2),
∴AO=BO=2,
又∵点C在第二、四象限坐标轴夹角平分线上,
∴∠BOC=∠COA=45°,
∴CO垂直平分AB(等腰三角形三线合一),
∴CA=CB,(线段垂直平分线上的点到线段两端的距离相等),
∵∠BAC=60°,
∴△ABC是等边三角形(有一个角等于60°的等腰三角形是等边三角形),
∴AB=AC=BC,
∴AB=
=
=2
;
假设CN=x,则CM=NO=x,NA=x-2,AC=2
.
在Rt△CNA中,∵CN2+NA2=AC2,
∴x2+(x-2)2=(2
)2,
整理得:x2-2x-2=0,
解得:x1=1+
,x2=1-
(不合题意舍去),
∴C点的坐标为:(-1-
,1+
);
当点在第四象限时,同理可得出:△ABC′是等边三角形,C′点的横纵坐标绝对值相等,
设C′点的坐标为(a,-a),
∴a2+(a+2)2=(2
)2,
解得:a1=-1-
(不合题意舍去),a2=-1+
,
C′点的坐标为:(-1+
,1-
),
故答案为:(-1+
,1-
),(-1-
,1+
).
 解:过点C作CM⊥y轴于点M,作CN⊥x轴于点N.
解:过点C作CM⊥y轴于点M,作CN⊥x轴于点N.∵点A(-2,0),点B(0,2),
∴AO=BO=2,
又∵点C在第二、四象限坐标轴夹角平分线上,
∴∠BOC=∠COA=45°,
∴CO垂直平分AB(等腰三角形三线合一),
∴CA=CB,(线段垂直平分线上的点到线段两端的距离相等),
∵∠BAC=60°,
∴△ABC是等边三角形(有一个角等于60°的等腰三角形是等边三角形),
∴AB=AC=BC,
∴AB=
| AO 2+BO2 |
| 4+4 |
| 2 |
假设CN=x,则CM=NO=x,NA=x-2,AC=2
| 2 |
在Rt△CNA中,∵CN2+NA2=AC2,
∴x2+(x-2)2=(2
| 2 |
整理得:x2-2x-2=0,
解得:x1=1+
| 3 |
| 3 |
∴C点的坐标为:(-1-
| 3 |
| 3 |
当点在第四象限时,同理可得出:△ABC′是等边三角形,C′点的横纵坐标绝对值相等,
设C′点的坐标为(a,-a),
∴a2+(a+2)2=(2
| 2 |
解得:a1=-1-
| 3 |
| 3 |
C′点的坐标为:(-1+
| 3 |
| 3 |
故答案为:(-1+
| 3 |
| 3 |
| 3 |
| 3 |
点评:此题主要考查了一次函数的综合应用以及等腰直角三角形的性质与判定和勾股定理等知识,结合图象得出△ABC是等边三角形,再利用勾股定理求出是解题关键,此题容易漏解,应利用数形结合认真分析.

练习册系列答案
相关题目
 14、如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO=
14、如图,已知点A,B,C在⊙O上,AC∥OB,∠BOC=40°,则∠ABO= 2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.