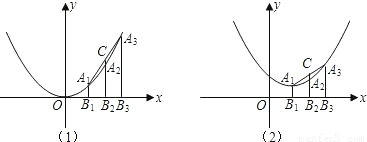题目内容
如图1,已知点A1,A2,A3是抛物线y=| 1 |
| 2 |
(1)在图(1)中,若点A1,A2,A3的横坐标依次为1,2,3,求线段CA2的长;
(2)若将抛物线改为y=
| 1 |
| 2 |
 2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
分析:(1)已知了A1,A2,A3三点的横坐标,可代入抛物线的解析式中求出A1B1,A2B2,A3B3的长,由于A1,A2,A3的横坐标是连续的三个整数,那么可用中位线定理来求出CB2的长,由此可根据CA2=CB2-A2B2,求出CA2的长.
(2)可先设出A1,A2,A3的横坐标依,由于这三个横坐标也是连续的整数,因此可按照(1)的方法进行求解.
(2)可先设出A1,A2,A3的横坐标依,由于这三个横坐标也是连续的整数,因此可按照(1)的方法进行求解.
解答:解:(1)∵点A1,A2,A3的横坐标依次为1,2,3,
∴A1B1=
×1=
,A2B2=
×4=2,A3B3=
×9=
;
由于A1B1∥A2B2∥A3B3,且B1B2=B2B3,
∴CB2=
(A1B1+A3B3)=
,
∴CA2=CB2-A2B2=
-2=
.
(2)设:点A1,A2,A3的横坐标依次为n-1,n,n+1,
∴A1B1=
(n-1)2-(n-1)+1,A2B2=
n2-n+1,A3B3=
(n+1)2-(n+1)+1;
由于A1B1∥A2B2∥A3B3,且B1B2=B2B3,
∴CB2=
(A1B1+A3B3)=
[
(n-1)2-(n-1)+1+
(n+1)2-(n+1)+1]=
n2-n+
,
∴CA2=CB2-A2B2=
n2-n+
-(
n2-n+1)=
.
∴A1B1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
由于A1B1∥A2B2∥A3B3,且B1B2=B2B3,
∴CB2=
| 1 |
| 2 |
| 5 |
| 2 |
∴CA2=CB2-A2B2=
| 5 |
| 2 |
| 1 |
| 2 |
(2)设:点A1,A2,A3的横坐标依次为n-1,n,n+1,
∴A1B1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由于A1B1∥A2B2∥A3B3,且B1B2=B2B3,
∴CB2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴CA2=CB2-A2B2=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了中位线定理,二次函数的应用等知识点,属于猜想类试题,解法不唯一,例如本题求CA2长还可以用B2点处两函数的差来求.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 x2上的三点,线段A1B1,A2B2,A3B3都垂直于x轴,垂足分别为点B1,B2,B3,延长线段B2A2交线段A1A3于点C.
x2上的三点,线段A1B1,A2B2,A3B3都垂直于x轴,垂足分别为点B1,B2,B3,延长线段B2A2交线段A1A3于点C. x2-x+1,如图2,点A1,A2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
x2-x+1,如图2,点A1,A2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.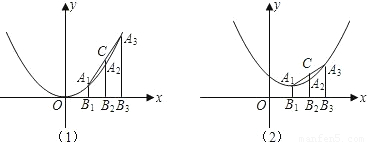
 x2上的三点,线段A1B1,A2B2,A3B3都垂直于x轴,垂足分别为点B1,B2,B3,延长线段B2A2交线段A1A3于点C.
x2上的三点,线段A1B1,A2B2,A3B3都垂直于x轴,垂足分别为点B1,B2,B3,延长线段B2A2交线段A1A3于点C. x2-x+1,如图2,点A1,A2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
x2-x+1,如图2,点A1,A2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
 x2上的三点,线段A1B1,A2B2,A3B3都垂直于x轴,垂足分别为点B1,B2,B3,延长线段B2A2交线段A1A3于点C.
x2上的三点,线段A1B1,A2B2,A3B3都垂直于x轴,垂足分别为点B1,B2,B3,延长线段B2A2交线段A1A3于点C. x2-x+1,如图2,点A1,A2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
x2-x+1,如图2,点A1,A2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.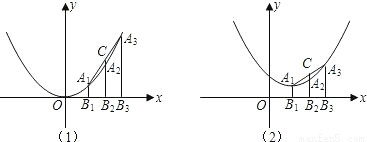
 x2上的三点,线段A1B1,A2B2,A3B3都垂直于x轴,垂足分别为点B1,B2,B3,延长线段B2A2交线段A1A3于点C.
x2上的三点,线段A1B1,A2B2,A3B3都垂直于x轴,垂足分别为点B1,B2,B3,延长线段B2A2交线段A1A3于点C. x2-x+1,如图2,点A1,A2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
x2-x+1,如图2,点A1,A2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.