题目内容
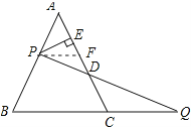
【题目】如图,P是等边△ABC的AB边上一点,过P作PE⊥AC于E,在BC的延长线上截取CQ=AP,连接PQ交AC于点D.
(1)若∠Q=28°,求∠EPD的度数;
(2)求证:PD=QD.

【答案】(1)58°;(2)证明见解析.
【解析】试题分析:作PF∥BC交AC于F,先证明△APF是等边三角形,得出AP=AF=PF.证出PF=CQ,由ASA证明△PFD≌△QCD,得出对应边相等即可.
试题解析:(1)解:∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∵∠Q=28°,
∴∠EDP=∠CDQ=∠ACB﹣∠Q=32°,
∵PE⊥AC,
∴∠PED=90°,
∴∠EPD=90°﹣∠EDP=58°;
(2)证明:作PF∥BC交AC于F,如图所示:
∴∠APF=∠B=60°,∠AFP=∠ACB=60°,
∠FPD=∠CQD,∠PFD=∠QCD,
∴∠APF=∠AFP=∠A=60°,
∴△APF是等边三角形,
∴AP=AF=PF.
∵CQ=AP,
∴PF=CQ,
在△PFD和△QCD中,
∠FPD=∠CQD,PF=CQ,∠PFD=∠QCD
∴△PFD≌△QCD(ASA),
∴PD=QD.

练习册系列答案
相关题目

