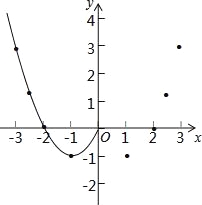题目内容
【题目】如图，△ABC中，∠B的平分线与∠C的外角的平分线交于P点，PD⊥AC于D，PH⊥BA于H，（1）若点P到直线BA的距离是5cm，求点P到直线BC的距离；（2）求证：点P在∠HAC的平分线上．
【答案】（1）5cm；（2）证明见解析.
【解析】试题分析：（1）过P作PF⊥BE于F，由于BP平分∠ABC，PH⊥BA，PF⊥BE，则根据角平分线的性质即可得到PH=PF=5cm；
（2）根据角平分线的性质得PF=PD，则PD=PH，于是根据到角的两边距离相等的点在这个角的平分线上得到AP平分∠HAD．
试题解析：（1）解：过P作PF⊥BE于F，如图，∵BP平分∠ABC，PH⊥BA于H，PF⊥BE于F，∴PH=PF=5cm，∴点P到直线BC的距离为5cm；（2）证明：∵CP平分∠ACE，PD⊥AC于D，
PF⊥BE于F，∴PF=PD，∴PD=PH，∴AP平分∠HAC．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究，探究过程如下，请补充完整．
（1）自变量x的取值范围是全体实数，x与y的几组对应值列表：
x | … | ﹣3 | － | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中m= ．
（2）根据上表数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分；
（3）观察函数图象，写出2条函数的性质；
（4）进一步探究函数图象发现：
①函数图象与x轴有 个交点，所对应的方程x2﹣2|x|=0有
②方程x2﹣2|x|=2有 个实数根．
