��Ŀ����
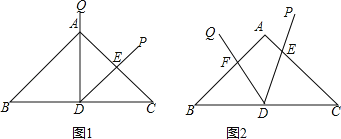
����Ŀ���ڵ�����ABC�У�AB=AC=10��BC=12��DΪ�ױ�BC���е㣬��DΪ����Ľǡ�PDQ=��B��
��1����ͼ1��������DQ������A��DP��AC���ڵ�E��ֱ��д�����CDE���Ƶ������Σ�
��2����ͼ2��������DQ��AB�ڵ�F��DP��AC���ڵ�E����AF=x��AEΪy����д��y��x�ĺ�����ϵʽ������Ҫ��д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£�����EF�����DEF���CDE��������˵�����ɣ�
���𰸡���1����1�����CDE���Ƶ�������Ϊ��ABD����ACD����ADE�����ɼ���������2��y=![]() ����3����DEF���CDE���ƣ����ɼ�����.
����3����DEF���CDE���ƣ����ɼ�����.
�����������������1���ɵ��������ε����ʵó���B=��C����ADB=��ADC=90���������ABD�ס�ACD��֤����PDQ=��C���ɡ�DAE=��CAD���ó���ADE�ס�ACD����֤����CDE�ס�CAD�����ɵó������
��2��֤����BDF�ס�CDE���ó���Ӧ�߳ɱ���![]() �����ɵó�y��x�ĺ�����ϵʽ��
�����ɵó�y��x�ĺ�����ϵʽ��
��3���ɣ�2����֪����BDF�ס�CDE���ó�![]() ֤��
֤��![]() ���ɡ�EDF=��C�����ɵó���DEF�ס�CED��
���ɡ�EDF=��C�����ɵó���DEF�ס�CED��
�����������1������CDE���Ƶ�������Ϊ��ABD����ACD����ADE���������£�
��AB=AC��DΪ�ױ�BC���е㣬
���B=��C��AD��BC��
���ADB=��ADC=90����
���ABD�ס�ACD��
�ߡ�PDQ=��B��
���PDQ=��C��
�֡ߡ�DAE=��CAD��
���ADE�ס�ACD��
�ߡ�CDE+��PDQ=90����
���C+��PDQ=90����
���CED=90��=��ADC��
�֡ߡ�C=��C��
���CDE�ס�CAD��
�����ABD�ס�ACD�ס�ADE�ס�CDE��
��2���ߡ�FDC=��B+��BDF��
��FDC=��FDE+��EDC��
���EDC=��BDF��
���BDF�ס�CDE��
��![]() ��
��
��DΪBC���е㣬
��BD=CD=6��
��![]()
��y=![]() ��
��
��3����DEF����CDE���ƣ��������£���ͼ��ʾ��
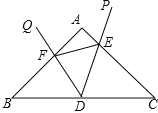
�ɣ�2����֪����BDF�ס�CDE��
��![]() ��
��
��BD=CD��
��![]() ��
��
�֡ߡ�EDF=��C��
���DEF�ס�CED��





