题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发沿
出发沿![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发沿
出发沿![]() 运动,如果
运动,如果![]() 、
、![]() 两点同时出发,
两点同时出发,![]() 的速度为1个单位/秒.
的速度为1个单位/秒.![]() 在
在![]() 上的速度为1个单位/秒,在
上的速度为1个单位/秒,在![]() 上的速度为
上的速度为![]() 个单位/秒.设出发时间为
个单位/秒.设出发时间为![]() ,记
,记![]() 的面积
的面积![]() 的函数图象为
的函数图象为![]() .
.

(1)当![]() 时,
时,![]() 的长是_________;
的长是_________;
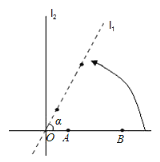
(2)若直线![]() 与
与![]() 有两个交点,则
有两个交点,则![]() 的取值范围为_________.
的取值范围为_________.
【答案】![]()
![]() 且
且![]()
【解析】
(1)当![]() 时,可得BP、BQ的长,利用勾股定理计算即可;
时,可得BP、BQ的长,利用勾股定理计算即可;
(2)分0≤x≤4和4<x≤8两种情况,利用三角形的面积公式找出y1关于x函数关系式,依此画出图象T,再逐一分析直线y2=x+b与T相切或过(0,0)、(8,4![]() )时b的值,结合图形即可得出结论.
)时b的值,结合图形即可得出结论.
解:(1)当x=1时,AP=BQ=1,
∵AB=BC=4,
∴BP=AB-AP=3,
∵∠B=90°,
∴在Rt△BPQ中,PQ=![]() ,
,
∴PQ的长为![]() ;
;
(2)当0≤x≤4时,y1=![]() PBBQ=
PBBQ=![]() (4-x)x=-
(4-x)x=-![]() x2+2x;
x2+2x;
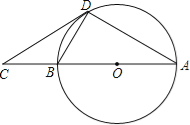
当4<x≤8时,过点Q作QD⊥BC与点D,如图1所示,
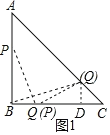
∵在△ABC中,∠B=90°,AB=BC=4,
∴∠ACB=45°,
∴QD=CQsin∠ACB=![]() ·
·![]() (x-4)=x-4,
(x-4)=x-4,
∴y1=![]() BPQD=
BPQD=![]() (x-4)(x-4)=
(x-4)(x-4)=![]() (x-4)2.
(x-4)2.
画出函数图象T,如图2所示.
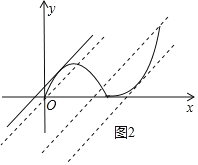
当直线y2=x+b与y![]() x2+2x(0≤x≤4)相切时,将y2=x+b代入y1=-
x2+2x(0≤x≤4)相切时,将y2=x+b代入y1=-![]() x2+2x中,
x2+2x中,
整理得:-![]() x2+x-b=0,
x2+x-b=0,
∵△=12-4×(-![]() )×(-b)=0,
)×(-b)=0,
∴b=![]() ;
;
当直线y2=x+b过点(0,0)时,有0=b;
当直线y2=x+b过点(8,8)时,有8=8+b,
解得:b=0;
当直线y2=x+b与y1=![]() (x-4)2(4<x≤8)相切时,
(x-4)2(4<x≤8)相切时,
将y2=x+b代入y1=![]() (x-4)2中,
(x-4)2中,
整理得:x2-10x+16-2b=0,
∵△=(-10)2-4×1×(16-2b)=0,
∴b=-![]() .
.
综上所述:当直线y2=x+b与T只有两个交点时,b的取值范围为![]() 且
且![]() .
.
故答案为:![]() 且
且![]() .
.

 名师点拨卷系列答案
名师点拨卷系列答案【题目】在10盒红色的笔芯中混放了若干支黑色的笔芯,每盒20支笔芯,每盒中混放入的黑色笔芯数如下表:
黑色笔芯数 | 0 | 1 | 4 | 5 | 6 |
盒数 | 2 | 4 | 1 | 2 | 1 |
下列结论:
①黑色笔芯一共有16支;
②从中随机取一盒,盒中红色笔芯数不低于14是必然事件;
③从中随机取一盒,盒中黑色笔芯数不超过4的概率为0.7;
④将10盒笔芯混在一起,从中随机抽取一支笔芯,恰好是黑色的概率是0.12.
其中正确的结论有()
A.1个B.2个C.3个D.4个
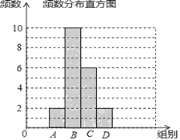
【题目】张老师把微信运动里“好友计步榜”排名前20的好友一天行走的步数做了整理,绘制了如下不完整的统计图表:
组别 | 步数分组 | 频率 |
A | x<6000 | 0.1 |
B | 6000≤x<7000 | 0.5 |
C | 7000≤x<8000 | m |
D | x≥8000 | n |
合计 | 1 |
根据信息解答下列问题:
(1)填空:m= ,n= ;并补全条形统计图;
(2)这20名朋友一天行走步数的中位数落在 组;(填组别)
(3)张老师准备随机给排名前4名的甲、乙、丙、丁中的两位点赞,请求出甲、乙被同时点赞的概率.