Question

【题目】在10盒红色的笔芯中混放了若干支黑色的笔芯，每盒20支笔芯，每盒中混放入的黑色笔芯数如下表：

黑色笔芯数	0	1	4	5	6
盒数	2	4	1	2	1

下列结论：

①黑色笔芯一共有16支；

②从中随机取一盒，盒中红色笔芯数不低于14是必然事件；

③从中随机取一盒，盒中黑色笔芯数不超过4的概率为0.7；

④将10盒笔芯混在一起，从中随机抽取一支笔芯，恰好是黑色的概率是0.12．

其中正确的结论有（）

A.1个B.2个C.3个D.4个

Answer 1

【答案】C

【解析】

根据表格的信息分别验证算出黑色笔芯的数量，由每盒黑色笔芯的数量可以算出每盒红色笔芯的数量，即可验证①②的正确性，再算出盒中黑色笔芯数不超过4的概率，即可判断③，用黑色的数量除以总的笔数，可验证④.

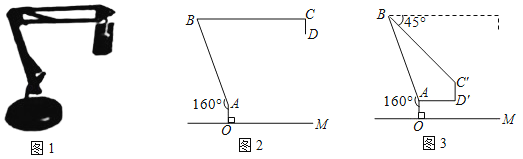
解：① 根据表格的信息，得到

黑色笔芯数=，

故①错误；

② 每盒笔芯的数量为20支，

∵每盒黑色笔芯的数量都≤6，

∴每盒红色笔芯≥14，

因此从中任取一盒，盒中红色笔芯数不低于14是必然事件，

故②正确；

③ 根据图表信息，得到黑色笔芯不超过4的一共有7盒，因此

从中随机取一盒，盒中黑色笔芯数不超过4的概率为7÷10=0.7

故③正确

④ 10盒笔芯一共有10×20=200（支），

由详解①知黑色笔芯共有24支，

将10盒笔芯混在一起，从中随机抽取一支笔芯，恰好是黑色的概率是24÷200=0.12，

故④正确；

综上有三个正确结论，

故答案为C.