Question

【题目】如图，四边形为半径为的的内接四边形，若，，，，则的直径为（ ）

A.4B.C.8D.

Answer 1

【答案】C

【解析】

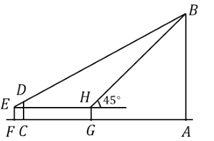
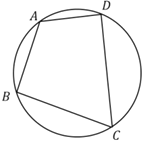
取的圆心O，连接OA、OB、OC、OD，过点O作OE⊥CD，OF⊥BC，OG⊥AD，垂足分别为E，F，G，先证得∠AOB＝60°及∠COD ＝120°，可得AOD+∠BOC＝180°，再利用垂径定理可得∠AOG+∠BOF＝90°，最后通过证△BOF≌△OAG得OF＝AG＝2，再利用勾股定理求解即可．

解：如图，取的圆心O，连接OA、OB、OC、OD，过点O作OE⊥CD，OF⊥BC，OG⊥AD，垂足分别为E，F，G，

∵OA＝OB＝AB＝R，

∴△AOB为等边三角形，

∴∠AOB＝60°，

∵OE⊥CD，，

∴，

在Rt△COE中，

∴∠COE＝60°，

∴∠COD＝2∠COE＝120°，

∴∠AOD+∠BOC＝360°﹣∠COD﹣∠AOB＝180°，

∵OF⊥BC，OG⊥AD，

∴AG＝AD＝2，BF＝BC＝2，∠AOG＝∠AOD，∠BOF＝∠BOC，

∴∠AOG+∠BOF＝（∠AOD+∠BOC）＝90°

又∵∠AOG+∠OAG＝90°，

∴∠BOF＝∠OAG，

∵∠BOF＝∠OAG，∠BFO＝∠OGA＝90°，OB＝OA，

∴△BOF≌△OAG（AAS），

∴OF＝AG＝2，

在Rt△BOF中，,

∴的直径＝2OB＝8，

故选：C．