题目内容
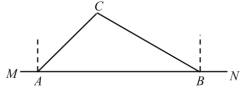
【题目】如图所示,直线![]() ,垂足为点
,垂足为点![]() 是直线
是直线![]() 上的两点,且
上的两点,且![]() .直线
.直线![]() 绕点
绕点![]() 按逆时针方向旋转,旋转角度为
按逆时针方向旋转,旋转角度为![]() .
.
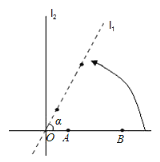
(1)当![]() 时,在直线
时,在直线![]() 上找点
上找点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形,此时
为顶角的等腰三角形,此时![]() _____.
_____.
(2)当![]() 在什么范围内变化时,直线
在什么范围内变化时,直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形,请用不等式表示
为顶角的等腰三角形,请用不等式表示![]() 的取值范围:_________.
的取值范围:_________.
【答案】(1)![]() 或
或![]() ;(2)45°≤
;(2)45°≤![]() ≤135°且
≤135°且![]() ≠90°
≠90°
【解析】
(1)先求出旋转后![]() 与
与![]() 的夹角,然后根据题意以点B为圆心,
的夹角,然后根据题意以点B为圆心,![]() 的长为半径作弧,与直线
的长为半径作弧,与直线![]() 的交点P即为所求,利用锐角三角函数即可求出BC和OC,再利用勾股定理求出PC,从而求出结论;
的交点P即为所求,利用锐角三角函数即可求出BC和OC,再利用勾股定理求出PC,从而求出结论;
(2)当由图可知:当BC≤AB且A、B、P不共线时,直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形,求出当BC=AB=
为顶角的等腰三角形,求出当BC=AB=![]() 时,
时,![]() 的度数,然后根据题意即可求出结论.
的度数,然后根据题意即可求出结论.
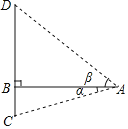
解:(1)当![]() 时,此时
时,此时![]() 与
与![]() 的夹角为90°-60°=30°
的夹角为90°-60°=30°
以点B为圆心,![]() 的长为半径作弧,与直线
的长为半径作弧,与直线![]() 的交点P即为所求,即BP=AB=
的交点P即为所求,即BP=AB=![]() ,过点B作BC⊥
,过点B作BC⊥![]() ,
,
BC=OB·sin30°=1<BP,OC=OB·cos30°=![]()
∴在直线![]() 上存在两个P点满足题意
上存在两个P点满足题意
根据勾股定理PC=![]()
∴OP=OC-PC或OP=OC+PC
∴OP=![]() 或
或![]()
故答案为:![]() 或
或![]() ;
;
(2)当由图可知:当BC≤AB且A、B、P不共线时,直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形,
为顶角的等腰三角形,
当BC=AB=![]() 时,
时,
sin∠BOC=![]()
∴∠BOC=45°
当点B在直线![]() 右侧时,
右侧时,
![]() 90°-∠BOC=45°;
90°-∠BOC=45°;
当点B在直线![]() 左侧时,
左侧时,
![]() 90°+∠BOC=135°;
90°+∠BOC=135°;
∵BC≤AB且A、B、P不共线时
∴45°≤![]() ≤135°且
≤135°且![]() ≠90°
≠90°
故答案为:45°≤![]() ≤135°且
≤135°且![]() ≠90°.
≠90°.

练习册系列答案
相关题目