Question

如图，在正方形ABCD中，AB=4，点E是边CD上的任意一点（不与C、D重合），将△ADE沿AE翻折至△AFE，延长EF交边BC于点G，连接AG．
（1）求证：△ABG≌△AFG；
（2）若设DE=x，BG=y，求y与x的函数关系式，并写出自变量x的取值范围；
（3）连接CF，若AG∥CF，求DE的长．

Answer 1

（1）证明：∵四边形ABCD为正方形，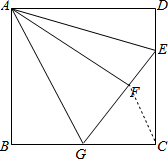
∴∠D=∠B=90°，AB=AD，
∵△ADE沿AE翻折至△AFE，
∴AD=AF，∠D=∠AFE=90°，
∴AB=AF，
在Rt△ABG和Rt△AFG中

AB=AF AG=AG

∴△ABG≌△AFG（HL）；

（2）∵△ADE≌△AFE，△ABG≌△AFG，
∴BG=FG，DE=FE，
∴EG=FE+FG，
∵AB=4，
∴BC=CD=4，
∵DE=x，BG=y，
∴EC=4-x，GE=x+y，GC=4-y，
∴在Rt△EGC中，CG²+CE²=GE²，
∴（4-y）²+（4-x）²=（x+y）²，
∴y=

-4x+16

x+4

（0＜x＜4）；

（3）∵AG∥CF，
∴∠AGB=∠FCG，∠AGF=∠GFC，
∵△ABG≌△AFG，
∴∠AGB=∠AGF，
∴∠FCG=∠GFC，
∴CG=GF，
∴y=4-y，解得y=2，
把y=2代入y=

-4x+16

x+4

得

-4x+16

x+4

=2，解得x=

4

3

，
∴DE=

4

3

．