题目内容
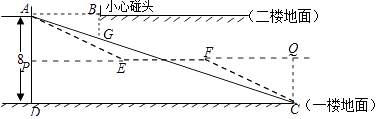
【题目】某大型购物商场在一楼和二楼之间安装自动扶梯AC,截面如图所示,一楼和二楼地面平行(即AB所在的直线与CD平行),层高AD为8米,∠ACD=20°,为使得顾客乘坐自动扶梯时不至于碰头,A、B之间必须达到一定的距离. (参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)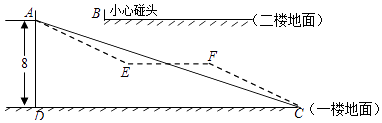
(1)要使身高2.26米的姚明乘坐自动扶梯时不碰头,那么A,B之间的距离至少要多少米?(精确到0.1米)
(2)如果自动扶梯改为由AE,EF,FC三段组成(如图中虚线所示),中间段EF为平台(即EF∥DC),AE段和FC段的坡度i=1:2,求平台EF的长度.(精确到0.1米)
【答案】
(1)解:连接AB,作BG⊥AB交AC于点G,则∠ABG=90°
∵AB∥CD,∴∠BAG=∠ACD=20°,
在Rt△ABG中, ![]() ,
,
∵BG=2.26,tan20°≈0.36,
∴ ![]() ,
,
∴AB≈6.3,
答:A、B之间的距离至少要6.3米
(2)解:设直线EF交AD于点P,作CQ⊥EF于点Q,
∵AE和FC的坡度为1:2,
∴ ![]() ,
,
设AP=x,则PE=2x,PD=8﹣x,
∵EF∥DC,
∴CQ=PD=8﹣x,
∴FQ=2(8﹣x)=16﹣2x,
在Rt△ACD中, ![]() ,
,
∵AD=8,∠ACD=20°,
∴CD≈22.22
∵PE+EF+FQ=CD,
∴2x+EF+16﹣2x=22.22,
∴EF=6.22≈6.2
答:平台EF的长度约为6.2米.
【解析】(1)连接AB,作BG⊥AB交AC于点G,在Rt△ABG中,利用已知条件求出AB的长即可;(2)设直线EF交AD于点P,作CQ⊥EF于点Q,设AP=x,则PE=2x,PD=8﹣x,在Rt△ACD中利用已知数据可求出CD的长,进而可求出台EF的长度.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A.抛物线于x轴的一个交点坐标为(﹣2,0)
B.抛物线与y轴的交点坐标为(0,6)
C.抛物线的对称轴是直线x=0
D.抛物线在对称轴左侧部分是上升的