题目内容
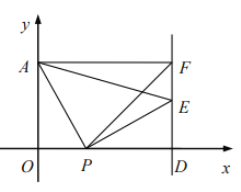
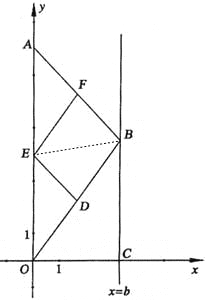
【题目】如图,在直角坐标系中,点A的坐标为(0,8),点 B(b,t)在直线x=b上运动,点D、E、F分别为OB、0A、AB的中点,其中b是大于零的常数.

(1)判断四边形DEFB的形状.并证明你的结论;
(2)试求四边形DEFB的面积S与b的关系式;
(3)设直线x=b与x轴交于点C,问:四边形DEFB能不能是矩形?若能.求出t的值;若不能,说明理由.
【答案】(1)平行四边形,证明见解析;(2)S=2b(b>0);(3)当0<b≤4时,四边形DEFB是矩形,这时,t=4±![]() ,当b>4时,四边形DEFB不是矩形.
,当b>4时,四边形DEFB不是矩形.
【解析】
解:(1)四边形DEFB是平行四边形.
证明:∵D、E分别是OB、OA的中点,
∴DE∥AB,同理,EF∥OB,
∴四边形DEFB是平行四边形;
(2)如图,连接BE,
S△AOB=![]() ×8×b=4b,
×8×b=4b,
∵E、F分别为OA、AB的中点,
∴S△AEF=![]() S△AEB=
S△AEB=![]() S△AOB=b,
S△AOB=b,
同理S△EOD=b,
∴S=S△AOB-S△AEF-S△ODE=4b-b-b=2b,
即S=2b(b>0);
(3)解法一:以E为圆心,OA长为直径的圆记为⊙E,
①当直线x=b与⊙E相切或相交时,若点B是切点或交点,则∠ABO=90°,由(1)知,四边形DEFB是矩形,
此时0<b≤4,可得△AOB∽△OBC,
∴![]()
![]()
,即OB2=OABC=8t,
在Rt△OBC中,OB2=BC2+OC2=t2+b2,
∴t2+b2=8t,
∴t2-8t+b2=0,
解得t=4±![]() ,
,
②当直线x=b与⊙E相离时,∠ABO≠90°,
∴四边形DEFB不是矩形,
综上所述:当0<b≤4时,四边形DEFB是矩形,这时,t=4±![]() ,当b>4时,四边形DEFB不是矩形;
,当b>4时,四边形DEFB不是矩形;
解法二:由(1)知,当∠ABO=90°时,四边形DEFB是矩形,
此时,Rt△OCB∽Rt△ABO,
∴![]() ,即OB2=OABC,
,即OB2=OABC,
又OB2=BC2+OC2=t2+b2,OA=8,BC=t(t>0),
∴t2+b2=8t,
∴(t-4)2=16-b2,
①当16-b2≥0时,解得t=4±![]() ,此时四边形DEFB是矩形,
,此时四边形DEFB是矩形,
②当16-b2<0时,t无实数解,此时四边形DEFB不是矩形,
综上所述:当16-b2≥0时,四边形DEFB是矩形,此时t=4±![]() ,当16-b2<0时,四边形DEFB不是矩形;
,当16-b2<0时,四边形DEFB不是矩形;
解法三:如图,过点A作AM⊥BC,垂足为M,

在Rt△AMB中,AB2=AM2+BM2=b2+(8-t)2,
在Rt△OCB中,OB2=OC2+BC2=b2+t2,
在Rt△OAB中,当AB2+OB2=OA2时,∠ABO=90°,则四边形DEFB为矩形,
∴b2+(8-t)2+b2+t2=82,
化简得t2-8t=-b2,配方得(t-4)2=16-b2,其余同解法二.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案