题目内容
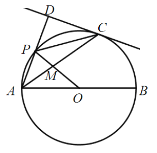
【题目】在平面直角坐标系中,点![]() 坐标为
坐标为![]() 轴上点
轴上点![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,过点
,过点![]() 作直线
作直线![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 直线
直线![]() 于
于![]() .
.
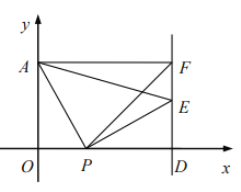
(1)当点![]() 是
是![]() 的中点时,求直线
的中点时,求直线![]() 的函数表达式.
的函数表达式.
(2)当![]() 时,求
时,求![]() 的面积.
的面积.
(3)在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,试用
?若存在,试用![]() 的代数式表示点
的代数式表示点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)3;(3)存在,
;(2)3;(3)存在,![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)证明Rt△APO≌Rt△PED,得到ED![]() PO,DO=OP+PD=OP+AO=3
PO,DO=OP+PD=OP+AO=3![]() ,求出点E(
,求出点E(![]() ,
,![]() ),P(
),P(![]() ,0),将点代入解析式即可求解;
,0),将点代入解析式即可求解;
(2)由(1)的全等可得到PD=3,DE=5,所以S△APE![]() 3×5
3×5![]() 3×3=3;
3×3=3;
(3)假设在直线l上存在点G,使得∠APO=∠PFD+∠PGD,由旋转可知△APO≌△PED,得到AP=PE,AO=PD=3,PO=ED=t;由AODF是矩形,得到DF=AO=3=PD.
①当P点在x轴负半轴,G点在x轴下方时,△GPE∽△GFP,得到![]() ,进而GP2=GEGF,得到G(3+t,
,进而GP2=GEGF,得到G(3+t,![]() );由对称性可得当P点在x轴负半轴,G点在x轴上方时G的坐标;
);由对称性可得当P点在x轴负半轴,G点在x轴上方时G的坐标;
②当P在x轴正半轴,G点在x轴下方时,△PFG∽△EFP,则有![]() ,得到G(3+t,
,得到G(3+t,![]() );由对称性可得当P在x轴正半轴,G点在x轴上方时G的坐标.
);由对称性可得当P在x轴正半轴,G点在x轴上方时G的坐标.
(1)∵线段AP绕点P顺时针旋转90°得到PE,
∴AP=PE,∠APE=90°.
∵∠APO+∠EPD=∠APO+∠OAP=90°,
∴∠EPD=∠OAP.
∵∠EDP=∠POA=90°,
∴Rt△APO≌Rt△PED(AAS)
∴OP=ED,AO=PD.
∵OA=3,点E是DF的中点,
∴ED![]() PO,
PO,
∴DO=OP+PD=OP+AO=3![]() ,
,
∴E(![]() ,
,![]() ),P(
),P(![]() ,0).
,0).
设直线PE的解析式为y=kx+b,
∴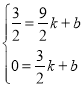 ,
,
∴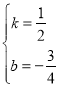 ,
,
∴y![]() ;
;
(2)∵Rt△APO≌Rt△PED,
∴OP=ED,AO=PD.
∵OA=3,OP=5,
∴PD=3,DE=5,
∴S△FPE![]() 3×5
3×5![]() 3×3=3;
3×3=3;
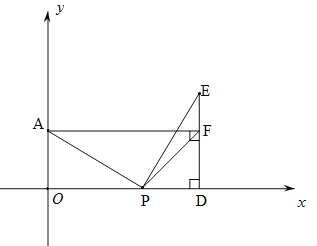
(3)假设在直线l上存在点G,使得∠APO=∠PFD+∠PGD,
由旋转可知△APO≌△PED,
∴AP=PE,AO=PD=3,PO=ED=t,∠APO=∠PED;
∵∠AOD=∠ODF=∠AFD=90°,
∴四边形AODF是矩形,
∴DF=AO=3,
∴PD=DF=3.
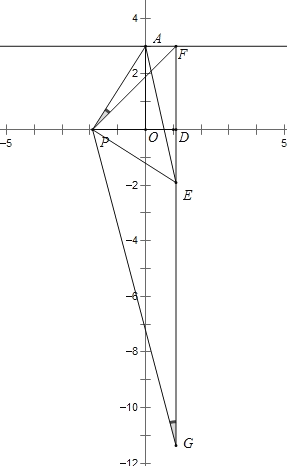
①当P点在x轴负半轴,G点在x轴下方时.
∵∠APO=∠PFD+∠PGD,∠APO=∠PED,
∴∠PED=∠PFD+∠PGD.
∵∠PED=∠GPE+∠PGD,
∴∠GPE=∠PFD.
∵∠PGE=∠PGE,
∴△GPE∽△GFP,
∴![]() ,
,
∴GP2=GEGF.
设G(m,y).
∵PD=3,
∴D(3+t,0),
∴m=3+t,
∴GE=t-y,GF=3-y,
∴![]() ,解得:y=
,解得:y=![]() ,
,
∴DG![]() ,
,
∴G(3+t,![]() );
);
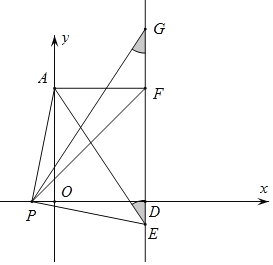
由对称性可知:当P在x轴负半轴,G点在x轴上方时,G(3+t,![]() );
);
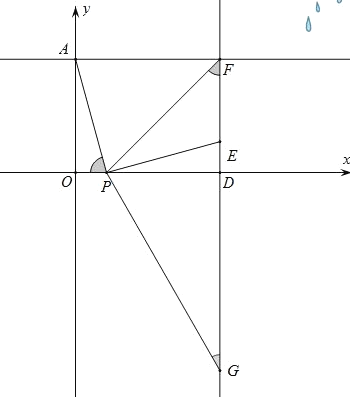
②当P在x轴正半轴,G点在x轴下方时.
∵∠APO=∠PFD+∠PGD,
∠PED=∠APO,
∴∠FPE=∠PGF,
∴△PFG∽△EFP,
∴![]() ,
,
∵△APO≌△PED,
∴OP=ED,AO=PD,
∴E(t+3,t),P(t,0),F(t+3,3),
∴![]() ,
,
∴FG![]() ,
,
∴G(3+t,![]() );
);
由对称性可知:当P在x轴正半轴,G点在x轴上方时,G(3+t,![]() );
);
综上所述:G(3+t,![]() )或G(3+t,
)或G(3+t,![]() )或G(3+t,
)或G(3+t,![]() )或G(3+t,
)或G(3+t,![]() ).
).