题目内容
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.
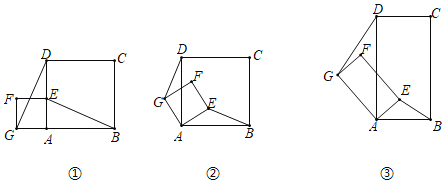
(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
【答案】(1)①BE=DG,②BE⊥DG;(2)数量关系不成立,DG=2BE,位置关系成立.理由见解析;(3)BG2+DE2=25.
【解析】
(1)先判断出△ABE≌△DAG,进而得出BE=DG,∠ABE=∠ADG,再利用等角的余角相等即可得出结论;
(2)先利用两边对应成比例夹角相等判断出△ABE∽△DAG,得出∠ABE=∠ADG,再利用等角的余角相等即可得出结论;
(3)如图④中,作ET⊥AD于T,GH⊥BA交BA的延长线于H.设ET=x,AT=y.利用勾股定理,以及相似三角形的性质即可解决问题.
(1)①如图②中,
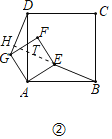
∵四边形ABCD和四边形AEFG是正方形,
∴AE=AG,AB=AD,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
在△ABE和△DAG中,
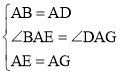 ,
,
∴△ABE≌△DAG(SAS),
∴BE=DG;
②如图2,延长BE交AD于T,交DG于H.
由①知,△ABE≌△DAG,
∴∠ABE=∠ADG,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG,
故答案为:BE=DG,BE⊥DG;
(2)数量关系不成立,DG=2BE,位置关系成立.
如图③中,延长BE交AD于T,交DG于H.

∵四边形ABCD与四边形AEFG都为矩形,
∴∠BAD=∠DAG,
∴∠BAE=∠DAG,
∵AD=2AB,AG=2AE,
∴![]() =
=![]() =
=![]() ,
,
∴△ABE∽△ADG,
∴∠ABE=∠ADG,![]() =
=![]() ,
,
∴DG=2BE,
∵∠ATB+∠ABE=90°,
∴∠ATB+∠ADG=90°,
∵∠ATB=∠DTH,
∴∠DTH+∠ADG=90°,
∴∠DHB=90°,
∴BE⊥DG;
(3)如图④中,作ET⊥AD于T,GH⊥BA交BA的延长线于H.设ET=x,AT=y.
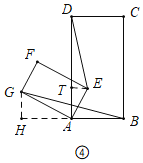
∵∠GAH+∠DAG=90°,∠BAE+∠DAG=90°,
∴∠GAH=∠BAE,
又∵∠GHA=∠ATE=90°,
∴△AHG∽△ATE,
∴![]() =2,
=2,
∴GH=2x,AH=2y,
∴4x2+4y2=4,
∴x2+y2=1,
∴BG2+DE2=(2x)2+(2y+2)2+x2+(4﹣y)2=5x2+5y2+20=25.