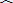题目内容
如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
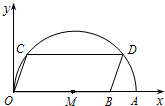

∵四边形OCDB是平行四边形,B(8,0),
∴CD∥OA,CD=OB=8
过点M作MF⊥CD于点F,则CF=
CD=4
过点C作CE⊥OA于点E,
∵A(10,0),
∴OE=OM-ME=OM-CF=5-4=1.
连接MC,则MC=
OA=5
∴在Rt△CMF中,由勾股定理得MF=
=
=3
∴点C的坐标为(1,3)
∴CD∥OA,CD=OB=8
过点M作MF⊥CD于点F,则CF=
| 1 |
| 2 |
过点C作CE⊥OA于点E,
∵A(10,0),
∴OE=OM-ME=OM-CF=5-4=1.
连接MC,则MC=
| 1 |
| 2 |
∴在Rt△CMF中,由勾股定理得MF=
| MC2-CF2 |
| 52-42 |
∴点C的坐标为(1,3)


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
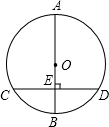
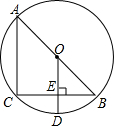
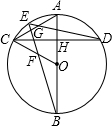 与弦AC相交于点G.
与弦AC相交于点G.