题目内容
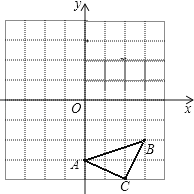
【题目】如图，在平面直角坐标系中，点O为坐标原点，△ABC是直角三角形，∠ACB=90°，点B、C都在第一象限内，CA⊥x轴，垂足为点A，反比例函数y1= 
的图象经过点B；反比例函数y2= 
的图象经过点C（ 
，m）．
（1）求点B的坐标；
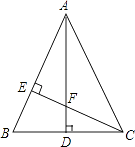
（2）△ABC的内切圆⊙M与BC，CA，AB分别相切于D，E，F，求圆心M的坐标．
【答案】
（1）
解：∵CA⊥x轴，∠ACB=90°，
∴CB∥x轴．
∵将C（ 
，m）代入函数y2= 
得：n= 
= ，
∴点C（ ， ）．
∴点B的纵坐标为 ．
∵将y1= 代入得： 
= ，解得；x=2 ，
∴点B的坐标为（2 ， ）
（2）
解：如图所示：连接ME、MD、MF．
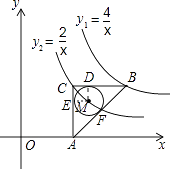
∵⊙M与BC，CA，AB分别相切于D，E，F，
∴ME⊥AC，MD⊥BC，MF⊥AB．
∴∠ECD=∠CDM=∠CEM=90°．
∴四边形CDME为矩形．
∵MD=ME，
∴四边形CDME为正方形．
∵在Rt△ACB中，AC= ，BC= ，
∴AB=2．
∵S△ACB= 
ACBC= （AC+BC+AB）r，
∴⊙M的半径= 
= 
= ﹣1．
∴点M的坐标为（2 ﹣1，1）
【解析】（1）先求得点C的坐标，然后根据平行于x轴上点纵坐标相等，可知点B的纵坐标，然后可求得点B的横坐标；（2）连接MD、ME、MF．由点B和点C的坐标可求得AC、BC的长，依据勾股定理可求得AB的长，然后在△ABC中利用面积法可求得圆M的半径，从而可求得点M的坐标．
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
