题目内容
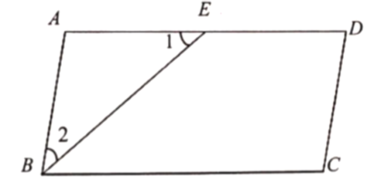
【题目】如图1, ![]() ABCD和
ABCD和![]() AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将
AEFG是两个能完全重合的平行四边形,现从AB与AE重合时开始,将![]() ABCD固定不动,
ABCD固定不动, ![]() AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当
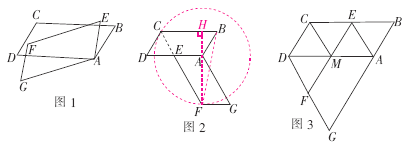
AEFG绕点A逆时针旋转,旋转角为α(0°<α<360°),AB=a,BC=2a;并发现:如图2,当![]() AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
AEFG旋转到点E落在AD上时,FE的延长线恰好通过点C.
探究一:
(1)在图2的情形下,求旋转角α的度数;
探究二:
(2)如图3,当![]() AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
AEFG旋转到点E落在BC上时,EF与AD相交于点M,连接CM,DF,请你判断四边形CDFM的形状,并给予证明;
探究三:
(3)如图1,连接CF,BF,在旋转过程中△BCF的面积是否存在最大的情形,如果存在,求出最大面积,如果不存在,请说明理由.
【答案】(1)α=120°;(2)四边形CDFM是菱形,证明见解析;(3)存在△BCF的面积最大的情形,S△BCF =![]() a2.
a2.
【解析】试题分析:(1)由平行四边形的性质知
∠D=∠B,AB=CD=a,可得∠D=∠DEC,由等角对等边知CD=CE,由AE=AB=a,AD=BC=2a,可得DE=CE,即可证得△CDE是等边三角形,∠D=60°,由两直线平行,同位角相等可得∠DAB=120°,即可求得α;
(2)由旋转的性质以及∠B=60°,可得△ABE是等边三角形,由平行线的判定以及两组对边分别平行的四边形是平行四边形可证四边形ABEM是平行四边形,再由由一组邻边相等的平行四边形是菱形即可得证;
(3)当点F到BC的距离最大时,△BCF的面积最大,由于点F始终在以A为圆心AF为半径的圆上运动,故当FG与⊙A相切时,点F到BC的距离最大,过点A作AH⊥BC于点H,连接AF,由题意知∠AFG=90°.由∠ABH=∠G=60°,AB=a,AG=2a,可得AH、AF的值.可求得点F到BC的最大距离.进而求得S△BCF的值.
试题解析:(1)∵四边形ABCD是平行四边形,
∴∠D=∠B,AB=CD=a,
∵∠AEF=∠B,∠AEF=∠DEC,
∴∠D=∠DEC,
∴CD=CE,
∵AE=AB=a,AD=BC=2a,
∴DE=CE.,
∴CD=CE=DE,
∴△CDE是等边三角形,
∴∠D=60°,
∵CD∥AB,
∴∠D+∠DAB=180°,
∴∠DAB=120°,
∴α=120°.;
(2)四边形CDFM是菱形.
证明:由旋转可得AB=AE,
∵∠B=60°,
∴△ABE是等边三角形,
∴∠BAE=60°,
∴∠BAG=∠BAE+∠GAE=60°+120°=180°,
∴点G,A,B在同一条直线上,
∴ME ∥AB,BE∥AM,
∴四边形ABEM是平行四边形,
∴AM=AB=ME,
∴CD=DM=MF,
∵CD ∥AB∥MF,
∴四边形CDFM是平行四边形,
∵∠D= 60°,CD=DM,
∴△CDM是等边三角形,
∴CD=DM,
∴四边形CDFM是菱形;
(3)存在△BCF的面积最大的情形.
∵CB的长度不变,
∴当点F到BC的距离最大时,△BCF的面积最大.
∵点F始终在以A为圆心AF为半径的圆上运动,
∴当FG与⊙A相切时,点F到BC的距离最大,
如图,过点A作AH⊥BC于点H,连接AF,
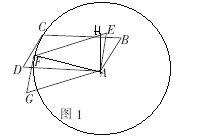
则∠AFG=90°.
∵∠ABH=∠G=60°,AB=a,AG=2a,
∴AH=AB×sin60°=![]() a,AF=AG×sin60°=
a,AF=AG×sin60°=![]() a.
a.
∴点F到BC的最大距离为![]() a+
a+ ![]() a=
a=![]() a.
a.
∴S△BCF=![]() ×2a×
×2a×![]() a=
a=![]() a2.
a2.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】问题呈现:我们知道反比例函数y=![]() (x>0)的图象是双曲线,那么函数y=
(x>0)的图象是双曲线,那么函数y=![]() +n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=
+n(k、m、n为常数且k≠0)的图象还是双曲线吗?它与反比例函数y=![]() (x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
(x>0)的图象有怎样的关系呢?让我们一起开启探索之旅……
探索思考:我们可以借鉴以前研究函数的方法,首先探索函数y=![]() 的图象.
的图象.
(1)填写下表,并画出函数y=![]() 的图象.
的图象.
①列表:
x | … | ﹣5 | ﹣3 | ﹣2 | 0 | 1 | 3 | … |
y | … | … |
②描点并连线.
(2)观察图象,写出该函数图象的两条不同类型的特征:
① ② ;
理解运用:函数y=![]() 的图象是由函数y=
的图象是由函数y=![]() 的图象向 平移 个单位,其对称中心的坐标为 .
的图象向 平移 个单位,其对称中心的坐标为 .
灵活应用:根据上述画函数图象的经验,想一想函数y=![]() +2的图象大致位置,并根据图象指出,当x满足 时,y≥3.
+2的图象大致位置,并根据图象指出,当x满足 时,y≥3.