题目内容
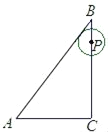
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与y轴交于点D,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.

(1)求k,b的值;
(2)请直接写出不等式kx+b﹣3x>0的解集;
(3)M为射线CB上一点,过点M作y轴的平行线交y=3x于点N,当MN=OD时,求M点的坐标.
【答案】(1)k=﹣1,b=4;(2)x<1;(3)M点坐标为(2,2).
【解析】
(1)先确定C点坐标,然后利用待定系数法求一次函数解析式,从而得到k、b的值;
(2)几何函数图象,写出直线y=kx+b在直线y=3x上方所对应的自变量的范围即可;
(3)先确定D点坐标,设点M的横坐标为m,则M(m,m+4),N(m,3m),则4m4=4,然后求出m即可得到M点坐标.
(1)当x=1时,y=3x=3,
∴C点坐标为(1,3).
直线y=kx+b经过(﹣2,6)和(1,3),
则![]() ,解得:k=﹣1,b=4;
,解得:k=﹣1,b=4;
(2)由图可知,不等式kx+b﹣3x>0的解集为x<1;
(3)当x=0时,y=﹣x+4=4,
∴D点坐标为(0,4),
∴OD=4.
设点M的横坐标为m,则M(m,﹣m+4),N(m,3m),
∴MN=3m﹣(﹣m+4)=4m﹣4
∵MN=OD,
∴4m﹣4=4,解得m=2.
即M点坐标为(2,2).

【题目】“端午节”期间,某商场购进A、B两种品牌的粽子共320袋,其中A品牌比B品牌多80袋.此两种粽子每袋的进价和售价如下表所示,已知销售八袋A品牌的粽子获利136元.(注;利润=售价-进价)
品牌 | A | B |
进价(元/袋) | m | 38 |
售价(元/袋) | 66 | 50 |
(1)试求出m的值.
(2)该商场购进A、B两种品牌的粽子各多少袋?
(3)该商场调整销售策略,A品牌的粽子每袋按原售价销售,B品牌的粽子每袋打折出售.如果购进的A、B两种品牌的粽子全部售出的利润不少于4360元,问B种品牌的粽子每袋最低打几折出售?
【题目】为了调查学生对数学知识的理解和应用,某校学生会专门针对七年级举办了“数学知识应用创新能力”测试,七年级的所有学生都参加了测试,试卷共有![]() 道题,每题
道题,每题![]() 分.测试结束后随机抽取了部分学生的测试成绩绘制出部分频数分布表和频数分布直方图,请结合图表完成下列各题:
分.测试结束后随机抽取了部分学生的测试成绩绘制出部分频数分布表和频数分布直方图,请结合图表完成下列各题:
组别 | 成绩 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
合计 |
|

(![]() )频数分布表中
)频数分布表中![]() 的值等于 ;
的值等于 ;
(![]() )请把频数分布直方图补充完整;
)请把频数分布直方图补充完整;
(![]() )若测试成绩不低于
)若测试成绩不低于![]() 分为优秀,请你估计七年级
分为优秀,请你估计七年级![]() 名学生成绩优秀的有多少人?
名学生成绩优秀的有多少人?