题目内容
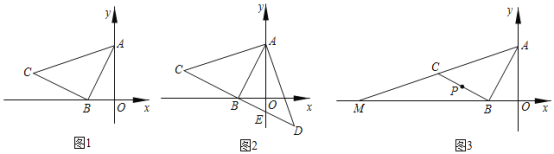
【题目】如图,在直角三角形ABC中,∠ACB=90°,AC=6,BC=8,点M是AB上的一点,点N是CB上的一点.
(1)若3BM=4CN.
①如图1,当CN=![]() 时,判断MN与AC的位置关系,并说明理由;
时,判断MN与AC的位置关系,并说明理由;
②如图2,连接AN,CM,当∠CAN与△CMB中的一个角相等时,求BM的值.
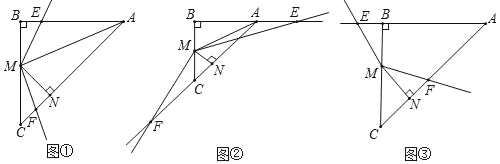
(2)当MN⊥AB时,将△NMB沿直线MN翻折得到△NMF,点B落在射线BA上的F处,设MB=x,△NMF与△ABC重叠部分的面积为y,求y关于x的函数表达式及x的取值范围.

【答案】(1)①MN∥AC;②BM=4或6;(2)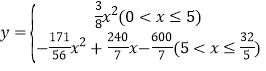 .
.
【解析】
(1)①结论:MN∥AC.只要证明![]() =
=![]() 即可;
即可;
②分两种情形当∠CAN=∠B时,当∠CAN=∠MCB时,分别构建方程求解即可;
(2)分两种情形:①如图3﹣1,当点F在线段AB上时,②如图3﹣2中,当点F在线段BA的延长线上时,分别利用相似三角形的性质根据函数即可;
(1)①在直角三角形ABC中,∵∠ACB=90°,AC=6,BC=8,∴AB=10.
∵3BM=4CN,∴![]() =
=![]() .
.
∵BM=![]() ,∴BN=BC﹣CN=8﹣
,∴BN=BC﹣CN=8﹣![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴MN∥AC,②∵∠CMB>∠CAB>∠CAN,∴∠CAN≠∠CAB,设CN=3k,BM=4k,当∠CAN=∠B时,可得△CAN∽△CBA,∴
,∴MN∥AC,②∵∠CMB>∠CAB>∠CAN,∴∠CAN≠∠CAB,设CN=3k,BM=4k,当∠CAN=∠B时,可得△CAN∽△CBA,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴k=
,∴k=![]() ,∴BM=6.
,∴BM=6.
当∠CAN=∠MCB时,如图2中,过点M作MH⊥CB,可得△BMH∽△BAC,∴![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() ,∴MH=
,∴MH=![]() k,BH=
k,BH=![]() k,∴CH=8﹣
k,∴CH=8﹣![]() k.
k.
∵∠CAN=∠MCB,∴tan∠CAN=tan∠MCB.
∵![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴k=1或k=0(舍去),∴k=1,∴BM=4.
,∴k=1或k=0(舍去),∴k=1,∴BM=4.
综上所述:BM=4或6.
(2)如图3﹣1,当点F在线段AB上时.
∵BM=x,△BMN∽△BCA,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴MN=
,∴MN=![]() x,BN=
x,BN=![]() x,∴y=
x,∴y=![]() ×x×
×x×![]() x=
x=![]() x2(0<x≤5);
x2(0<x≤5);
如图3﹣2中,当点F在线段BA的延长线上时,过点C作CL∥BF交ON的延长线于点L,∴△CLN∽△BFN,∴![]() =
=![]() .
.
∵△BMN∽△BCA,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴BN=
,∴BN=![]() x,CN=8﹣
x,CN=8﹣![]() x,∴
x,∴![]() =
=![]() ,∴CL=
,∴CL=![]() ﹣﹣2x.
﹣﹣2x.
∵△CLO∽△AFO,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴CO=
,∴CO=![]() ﹣2x),∴y=S△ABC﹣S△BMN﹣S△CON=24﹣
﹣2x),∴y=S△ABC﹣S△BMN﹣S△CON=24﹣![]() x2﹣
x2﹣![]() (8﹣
(8﹣![]() x)
x)![]() ﹣2x),∴y=﹣
﹣2x),∴y=﹣![]() x2+
x2+![]() x﹣
x﹣![]() (5<x≤
(5<x≤![]() ).
).
综上所述: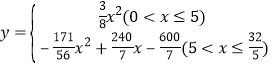 .
.

【题目】某超市第一次用![]() 元购进甲、乙两种商品,其中甲商品件数的
元购进甲、乙两种商品,其中甲商品件数的![]() 倍比乙商品件数的
倍比乙商品件数的![]() 倍多
倍多![]() 件,甲、乙两种商品的进价和售价如下表(利润=售价-进价)
件,甲、乙两种商品的进价和售价如下表(利润=售价-进价)
甲 | 乙 | |
进价(元/件) | 20 | 28 |
售价(元/件) | 26 | 40 |
(1)该超市第一次购进甲、乙两种商品的件数分别是多少?
(2)该超市将第一次购进的甲、 乙两种商品全部卖出后一共可获得多少利润?
(3)该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的![]() 倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多
倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多![]() 元,则第二次乙商品是按原价打几折销售的?
元,则第二次乙商品是按原价打几折销售的?