题目内容
在直角坐标系xoy中,已知点P是反比例函数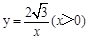 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
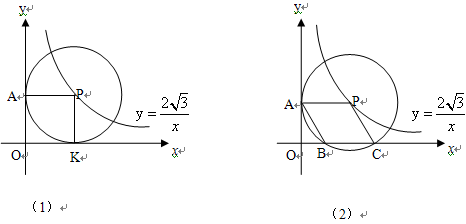
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B、C.当四边形ABCP是菱形时,求出点A、B、C的坐标.
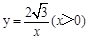 图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.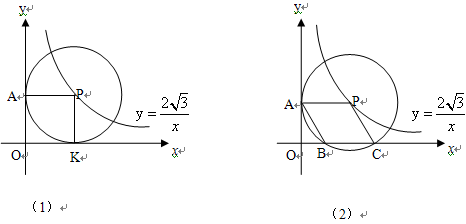
(1)如图1,⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
(2)如图2,⊙P运动到与x轴相交,设交点为B、C.当四边形ABCP是菱形时,求出点A、B、C的坐标.
(1)四边形OKPA是正方形.理由见解析(2)A(0, ),B(1,0) C(3,0)
),B(1,0) C(3,0)
 ),B(1,0) C(3,0)
),B(1,0) C(3,0)解:(1)∵⊙P分别与两坐标轴相切
∴ PA⊥OA,PK⊥OK
∴∠PAO=∠OKP=90°,而∠AOK=90°
∴四边形OKPA是矩形,而PA=PK
∴四边形OKPA是正方形
(2)连接PB,设点P的横坐标为x,则其纵坐标为 .
.
过点P作PG⊥BC于G,

∵四边形ABCP为菱形
∴BC="PC=" PA= AB,而PA=" PB" = PC
∴△PBC是等边三角形
在Rt△PBG中,∠PBG=60°,PB=PA=x
PG= .sin60°=
.sin60°= ,即
,即
解得:x=±2(负值舍去)∴ PG= ,PA=BC=2
,PA=BC=2
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1
∴OB=OG-BG=1,OC=OG+GC=3
∴ A(0, ),B(1,0) C(3,0).
),B(1,0) C(3,0).
(1)四边形OKPA是正方形.当⊙P分别与两坐标轴相切时,PA⊥y轴,PK⊥x轴,x轴⊥y轴,且PA=PK,可判断结论;
(2)连接PB,设点P(x, ),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=
),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=  ,利用sin∠PBG="PG/PB" ,列方程求x即可.
,利用sin∠PBG="PG/PB" ,列方程求x即可.
∴ PA⊥OA,PK⊥OK
∴∠PAO=∠OKP=90°,而∠AOK=90°
∴四边形OKPA是矩形,而PA=PK
∴四边形OKPA是正方形
(2)连接PB,设点P的横坐标为x,则其纵坐标为
 .
.过点P作PG⊥BC于G,

∵四边形ABCP为菱形
∴BC="PC=" PA= AB,而PA=" PB" = PC
∴△PBC是等边三角形
在Rt△PBG中,∠PBG=60°,PB=PA=x
PG=
 .sin60°=
.sin60°= ,即
,即
解得:x=±2(负值舍去)∴ PG=
 ,PA=BC=2
,PA=BC=2易知四边形OGPA是矩形,PA=OG=2,BG=CG=1
∴OB=OG-BG=1,OC=OG+GC=3
∴ A(0,
 ),B(1,0) C(3,0).
),B(1,0) C(3,0).(1)四边形OKPA是正方形.当⊙P分别与两坐标轴相切时,PA⊥y轴,PK⊥x轴,x轴⊥y轴,且PA=PK,可判断结论;
(2)连接PB,设点P(x,
 ),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=
),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=  ,利用sin∠PBG="PG/PB" ,列方程求x即可.
,利用sin∠PBG="PG/PB" ,列方程求x即可.
练习册系列答案
相关题目
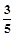 ,tan37°=
,tan37°=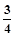 ,sin48°=
,sin48°=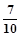 ,tan48°=
,tan48°=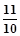 )
)


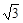 ≈1.732,结果保留整数).
≈1.732,结果保留整数).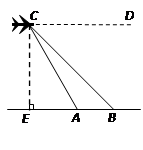

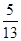 ,BC=24,则AC=__________.
,BC=24,则AC=__________.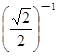 -2tan45°+(
-2tan45°+(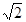 -1)0+22012×0.52012.
-1)0+22012×0.52012.