题目内容
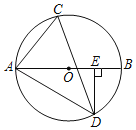
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)若CE=2,BE=1,求BD长.
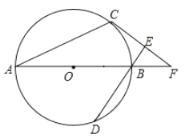
【答案】(1)见解析;(2)BD=3
【解析】
(1)连结OC,由于∠A=∠OCA,则根据三角形外角性质得∠BOC=2∠A,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)过点O作OG⊥DE,垂足为G,则可证四边形OCEG是矩形,可得OG=CE=2,OC=GE=1+GB,根据勾股定理可求GB的长,根据垂径定理可求BD的长.
解:(1)如图:连结OC,
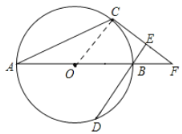
∵OA=OC,
∴∠A=∠OCA,
∴∠BOC=∠A+∠OCA=2∠A,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)如图:过点O作OG⊥DE,垂足为G
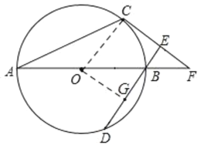
∵OG⊥DE,OC⊥CE,DE⊥CE
∴四边形OCEG是矩形
∴OG=CE=2,OC=GE=1+GB
在Rt△OGB中,OB2=OG2+GB2.
∴(1+GB)2=4+GB2.
∴GB=![]() ,
,
∵OG⊥DB
∴BD=2GB=3

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
【题目】已知二次函数![]() ,
,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断:
①抛物线![]() 的顶点为
的顶点为![]() ;
;
②![]() ;
;
③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;
;
④![]() .
.
其中,正确的有___________________