题目内容
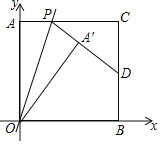
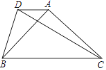
【题目】如图，在△ABC中，∠BAC=90°，AB=AC，DA∥BC，tan∠DBA= 
，若CD=2 
，则线段BC的长为________．
【答案】6 
【解析】
过D作DE⊥AB于E，DF⊥BC于F，根据等腰直角三角形的性质得到∠ABC=45°，根据平行线的性质得到∠DAE=∠ABC=45°，设AE=DE=x，由tan∠DBA=
，得到BE=2x，根据勾股定理得到BD=
x，AB=AC=3x，求得BC=3x，根据勾股定理得到DF2+CF2=CD2，即（
x）2+（
x）2=（2
）2，于是得到结论．
过D作DE⊥AB于E，DF⊥BC于F，
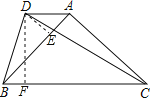
∵∠BAC=90°，AB=AC，
∴∠ABC=45°，
∵DA∥BC，
∴∠DAE=∠ABC=45°，
∴AE=DE，
设AE=DE=x，
∵tan∠DBA=，
∴BE=2x，
∴BD=x，AB=AC=3x，
∴BC=3x，
∴DF=x，
∴BF=
x，
∴CF=x，
∵DF2+CF2=CD2，
∴（x）2+（x）2=（2）2，
∴x=2，
∴BC=6．
故答案为：6.
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
【题目】为了了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查，已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
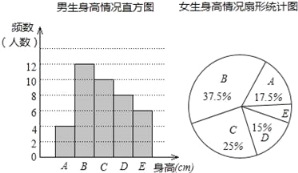
身高情况分组表（单位：cm）
组别 | 身高 |
A | x＜160 |
B | 160≤x＜165 |
C | 165≤x＜170 |
D | 170≤x＜175 |
E | x≥175 |
根据图表提供的信息，回答下列问题：
（1）样本中，男生的身高众数在 组，中位数在 组；
（2）样本中，女生身高在E组的人数有 人；
（3）已知该校共有男生600人，女生480人，请估计身高在165≤x＜175之间的学生约有多少人？
