题目内容
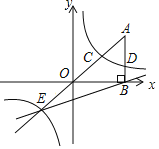
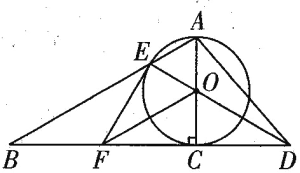
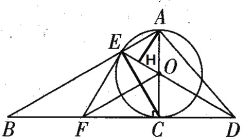
【题目】如图，以RtABC的直角边AC为直径作O交斜边AB于点E，连接EO并延长交BC的延长线于点D，作OF//AB交BC于点F，连接EF、EC.
（1）求证：OFCE；
（2）求证：EF是O的切线；
（3）若O的半径为3，EAC60，求tanADE
【答案】（1）见解析；（2）见解析；（3）
.
【解析】
（1）根据圆周角定理与平行线的性质即可证明；（2）易证EOF ≌ COF，即可证明EOF 90，则得证；(3) 过点 A，作 AH EO于点H，易证AOE 为等边三角形，故可求出
，再根据三角函数的定义即可求解.
解：（1）连接EC AC为直径，
AEC 90，
又OF // AB,OF CE
（2）OA OE,OAE OEA
又OF // AB,EAO FOC, AEO EOF
EOF COF , 又OE OC，OF为公共边
EOF ≌ COF (SAS )
EOF COF 90, 又OE为半径，∴EF为O的切线
（3）过点 A，作 AH EO于点H
EAC 60, OA OE,AOE 为等边三角形
，
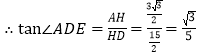
练习册系列答案
相关题目
