题目内容
【题目】已知二次函数解析式为y＝2x2﹣4x﹣6．
（1）写出抛物线的开口方向，顶点M坐标，对称轴，最值；
（2）求抛物线与x轴交点A，B与y轴的交点C的坐标；
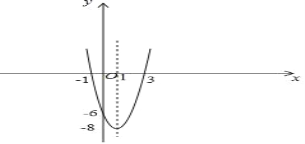
（3）作出函数的图象；
（4）观察图象：x为何值时，y随x的增大而增大；
（5）观察图象：当x何值时，y＞0；当x何值时，y＝0；当x何值时，y＜0．
【答案】（1）抛物线的开口向上，
；
；
.（2）A（﹣1，0），B（3，0），（0，﹣6）；（3）见解析；（4）当x＞1时y随x的增大而增大；（5）当x＜﹣1或x＞3时，y＞0；当x＝﹣1或x＝3时y＝0；当﹣1＜x＜3时y＜0．
【解析】
（1）将函数解析式化为顶点式即可解答本题；
（2）根据函数解析式可以求得与x轴和y轴的交点，本题得以解决；
（3）根据（1）、（2）中求得的点的坐标可以画出相应的函数图象；
（4）根据图象可以解答本题；
（5）根据图象可以解答本题．
（1）∵二次函数解析式为y＝2x2﹣4x﹣6＝2（x﹣1）2﹣8，
∴抛物线的开口向上，顶点M的坐标为（1，﹣8），对称轴是直线x＝1，最小值是y＝﹣8；
（2）∵二次函数解析式为y＝2x2﹣4x﹣6，
∴当x＝0时，y＝﹣6，当y＝0时，x1＝3，x2＝﹣1，
∴点A的坐标为（﹣1，0），点B的坐标为（3，0），点C的坐标为（0，﹣6）；
（3）函数图象如右图所示；
（4）由图象可知，当x＞1时y随x的增大而增大；
（5）由图象可知，当x＜﹣1或x＞3时，y＞0；
当x＝﹣1或x＝3时y＝0；
当﹣1＜x＜3时y＜0．
练习册系列答案
相关题目
