题目内容
【题目】如图,![]() 是半径为
是半径为![]() 的⊙
的⊙![]() 的直径,直线
的直径,直线![]() 与
与![]() 所在直线垂直,垂足为
所在直线垂直,垂足为![]() ,
,![]() ,点
,点![]() 是⊙
是⊙![]() 上异于
上异于![]() 、
、![]() 的动点,直线
的动点,直线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() 两点.
两点.
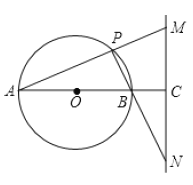
(1)当点![]() 为
为![]() 中点时,连接
中点时,连接![]() ,
,![]() ,判断直线
,判断直线![]() 与⊙
与⊙![]() 是否相切并说明理由.
是否相切并说明理由.
(2)点![]() 是⊙
是⊙![]() 上异于
上异于![]() 、
、![]() 的动点,以
的动点,以![]() 为直径的动圆是否经过一个定点,若是,请确定该定点的位置;若不是,请说明理由.
为直径的动圆是否经过一个定点,若是,请确定该定点的位置;若不是,请说明理由.
【答案】(1)CP为⊙O切线,理由详见解析;(2)以 MN 为直径的动圆过定点D,CD=![]()
【解析】
(1)如图1,根据同角的余角相等可得:∠AMC=∠ABP=∠OPB,从而得OP⊥PC,可知:直线PC与⊙O相切;
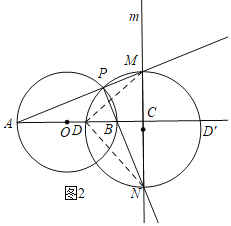
(2)如图2,设该圆与AC的交点为D,连接DM、DN,证△MDC∽△DNC得比例式,同理证△ACM∽△NCB,得DC的长,则以MN为直径的一系列圆经过定点D,此顶点D在直线AB上且CD的长为![]() ,同理在MN的右侧 还有一个点D',到C的距离也是
,同理在MN的右侧 还有一个点D',到C的距离也是![]() ..
..
(1)直线PC与⊙O相切,
理由是:如图所示:
∵AC⊥MN,
∴∠ACM=90°,
∴∠A+∠AMC=90°,
∵AB是⊙O的直径,
∴∠APB=∠NPM=90°,
∴∠PNM+∠AMC=90°=∠A+∠ABP,
∴∠ABP=∠AMC,
∵OP=OB,
∴∠ABP=∠OPB,
Rt△PMN中,C为MN的中点,
∴PC=CN,
∴∠PNM=∠NPC,
∴∠OPC=∠OPB+∠NPC=∠ABP+∠PNM=∠AMC+∠PNM=90°,
即OP⊥PC,
∴直线PC与⊙O相切;
(2)如图2,设该圆与AC的交点为D,连接DM、DN,
∵MN为直径,
∴∠MDN=90°,
则∠MDC+∠NDC=90°,
∵∠DCM=∠DCN=90°,
∴∠MDC+∠DMC=90°,
∴∠NDC=∠DMC,
则△MDC∽△DNC,
∴![]() ,即DC2=MCNC
,即DC2=MCNC
∵∠ACM=∠NCB=90°,∠A=∠BNC,
∴△ACM∽△NCB,
∴![]() ,即MCNC=ACBC;
,即MCNC=ACBC;
即ACBC=DC2,
∵AC=AO+OC=2+3=5,BC=3-2=1,
∴DC2=5,
∴DC=![]() ,
,
∵MN⊥DD',
∴D'C=DC=![]() ,
,
∴以MN为直径的一系列圆经过两个定点D和D',此定点在C的距离都是![]() .
.


 阅读快车系列答案
阅读快车系列答案