Question

【题目】如图，在Rt△POQ中，OP=OQ=4，M是PQ中点，∠P=∠Q=45°，将一三角尺的直角顶点放在点M处，以M为旋转中心旋转三角尺，三角尺的两直角边与△POQ的两直角边分别交于点A、B.试说明：MA=MB.

+

Answer 1

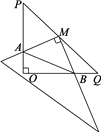【答案】说明见解析

【解析】试题分析：过点M作ME⊥PO，MF⊥QO，可得四边形OEBF是矩形，根据三角形的中位线定理可得ME=MF，再根据同角的余角相等可得再利用“角边角”证明和全等，根据全等三角形对应边相等即可证明；

试题解析：过点M作ME⊥PO，MF⊥QO，

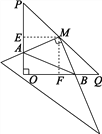
∴∠PEM=∠QFM=90°，又∵∠P=∠Q=45°，

∴∠PME=∠QMF=45°，∠EMF=90°，

又∵PM=QN，

∴△PME≌△QMF，∴EM=FM，

∵∠EMF=∠AMB=90°，

∴∠EMA=∠FMB，

又∵EM=FM，∠AEM=∠BFM=90°，

∴△AEM≌△BFM(ASA)，

∴MA=MB.