题目内容
【题目】已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.
(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
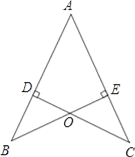
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
【答案】
(1)
证明:(1)①如图1,

∵AB⊥AD,AE⊥AC,
∴∠BAD=90°,∠CAE=90°,
∴∠1=∠2,
在△ABC和△ADE中,
∵ 
∴△ABC≌△ADE(SAS);
②如图1 ,
∵△ABC≌△ADE,
∴∠AEC=∠3,
在Rt△ACE中,∠ACE+∠AEC=90°,
∴∠BCE=90°,
∵AH⊥CD,AE=AC,
∴CH=HE,
∵∠AHE=∠BCE=90°,
∴BC∥FH,
∴ ![]() =1,
=1,
∴BF=EF;
(2)
解:结论仍然成立,理由是:
如图2所示,

过E作MN⊥AH,交BA、CD延长线于M、N,
∵∠CAE=90°,∠BAD=90°,
∴∠1+∠2=90°,∠1+∠CAD=90°,
∴∠2=∠CAD,
∵MN∥AH,
∴∠3=∠HAE,
∵∠ACH+∠CAH=90°,∠CAH+∠HAE=90°,
∴∠ACH=∠HAE,
∴∠3=∠ACH,
在△MAE和△DAC中,
∵ 
∴△MAE≌△DAC(ASA),
∴AM=AD,
∵AB=AD,
∴AB=AM,
∵AF∥ME,
∴ ![]() =1,
=1,
∴BF=EF.
【解析】(1)①利用SAS证全等;
②易证得:BC∥FH和CH=HE,根据平行线分线段成比例定理得BF=EF,也可由三角形中位线定理的推论得出结论.
(2)作辅助线构建平行线和全等三角形,首先证明△MAE≌△DAC,得AD=AM,根据等量代换得AB=AM,根据②同理得出结论.本题考查了全等三角形的性质和判定,平行线分线段成比例的性质,本题的关键是能正确找出全等三角形;在几何图形中证明线段相等或已知线段相等的一般思路是:①证明相等线段所在的三角形全等;②利用相等线段的比值为1证相等.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?