题目内容
【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1 , 0),B(x2 , 0),抛物线的顶点为C,显然△ABC为等腰三角形.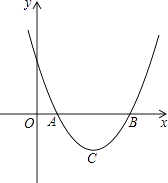
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值.
【答案】
(1)
解:当△ABC为等腰直角三角形时,过C作CD⊥AB于D,则AB=2CD;
∵抛物线与x轴有两个交点,
∴△>0,
∴|b2﹣4ac|=b2﹣4ac,
∵AB= ![]() ,
,
又∵CD= ![]() (a≠0),
(a≠0),
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴b2﹣4ac= ![]() ,
,
∵b2﹣4ac≠0,
∴b2﹣4ac=4
(2)
解:如图,当△ABC为等边三角形时,
由(1)可知CE= ![]() AE=
AE= ![]() AB,
AB,
∴ ![]() =
= ![]() ×
× ![]() ,
,
∵b2﹣4ac>0,
∴ ![]() =
= ![]() ,
,
∴b2﹣4ac=12.
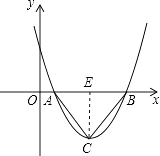
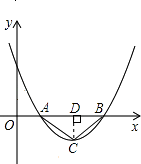
【解析】(1)由于抛物线与x轴有两个不同的交点,所以b2﹣4ac>0;可求得线段AB的表达式,利用公式法可得到顶点C的纵坐标,进而求得斜边AB上的高(设为CD),若△ABC为等腰直角三角形,那么AB=2CD,可根据这个等量关系求出b2﹣4ac的值;(2)当△ABC为等边三角形时,解直角△ACE,得CE= ![]() AE=
AE= ![]() AB,据此列出方程,解方程求出b2﹣4ac的值.
AB,据此列出方程,解方程求出b2﹣4ac的值.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案【题目】初三数学课本上,用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣15.5 | ﹣5 | ﹣3.5 | ﹣2 | ﹣3.5 | … |
根据表格上的信息回答问题:该二次函数y=ax2+bx+c在x=3时,y= .
【题目】甲、乙两名学生进行射击练习,两人在相同条件下各射靶![]() 次,将射击结果作统计分析如下:
次,将射击结果作统计分析如下:
命中环数 |
|
|
|
|
|
| 平均数 | 众数 | 方差 | |
甲命中环数的次数 |
|
|
|
|
|
|
|
|
| |
乙命中环数的次数 |
|
|
|
|
|
| ________ | ________ | ________ |
![]() 请你完成上表中乙进行射击练习的相关数据;
请你完成上表中乙进行射击练习的相关数据;
![]() 根据你所学的统计知识,利用上面提供的数据评价甲、乙两人的射击水平.
根据你所学的统计知识,利用上面提供的数据评价甲、乙两人的射击水平.